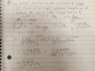Electric field of ring of charge/washer of charge/disk of charge

[cookiemnstr510510]

Homework Statement

Homework Equations

charge density equations, electric field equations,

The Attempt at a Solution

My attempts are attached. The attachment labeled A, is part A. Part B took a lot of paper so there are two attachments labeled B1 and B2. It is really B and C that I am struggling with. Not sure if I am on the right track or if it is correct. Any help would be much appreciated!

A little more thought: All the problems I have done in the back of my physics textbook are not like part B. I can find the electric field of a disk without a cut out in it. My thought process of finding the electric field with a cut out in it is integrating from the smaller radius to the larger radius. However, The total area of the washer is piR2^2-piR1^2. I plugged this result into my surface charge density toward the end of my solution.

My attempt at solution C:
Washer has charge +Q, Ring has radius 2R2, Lambda=Q/L
Clearly the charge on the ring has to be negative
therefore Lambda on ring is: -Q/4piR2

Thanks in advanced[/B]

 

[Charles Link]

B1.JPG is correct. APG is also correct. Combine the two results and set it equal to zero with $z=3 R_2$. $\\$ In APG, you must set $Q=2 \pi (2R_2) \lambda=4 \pi R_2 \lambda$, and $R=2R_2$. (This is not the same $Q$ that you have in B1.JPG. so call it $Q'$. It turns out $Q' \neq Q$. ). $\\$ Suggestion: Call the $E_z$ at $z=3R_2$ by $E_1$ and $E_2$. You must have $E_1+E_2=0$, which means $E_2=-E_1$. Your answer above for $\lambda$ is incorrect, but the rest is really just algebra. Try again. I'll be happy to check your result. (Note: $E_2$ is an expression that has $\lambda$ in it, and $E_1$ has $Q$ in it. Using $E_2=-E_1$, solve for $\lambda$).

 

[cookiemnstr510510]

Thank you! I’ll work on it tomorrow and respond! Appreciate it

 

[cookiemnstr510510]

B1.JPG is correct. APG is also correct. Combine the two results and set it equal to zero with $z=3 R_2$. $\\$ In APG, you must set $Q=2 \pi (2R_2) \lambda=4 \pi R_2 \lambda$, and $R=2R_2$. (This is not the same $Q$ that you have in B1.JPG. so call it $Q'$. It turns out $Q' \neq Q$. ). $\\$ Suggestion: Call the $E_z$ at $z=3R_2$ by $E_1$ and $E_2$. You must have $E_1+E_2=0$, which means $E_2=-E_1$. Your answer above for $\lambda$ is incorrect, but the rest is really just algebra. Try again. I'll be happy to check your result. (Note: $E_2$ is an expression that has $\lambda$ in it, and $E_1$ has $Q$ in it. Using $E_2=-E_1$, solve for $\lambda$).

Okay, So I am finally looking at your response in more detail.
What I have so far is:
E2 is electric field for concentric ring
E2=(k)(lambda)(dl)/r^2
I see what you mean that E1 + E2 has to = 0. Therefore E2=-E1. I guess my question is did I already solve for E1 in image B1JPG?

 

[Charles Link]

Yes, that is $E_1$ and it is correct.$\\$ And $E_2$ is correct in A1JPG, but you need to set $R=2R_2$, and $Q =2 \pi (2R_2) \lambda$. (As previously mentioned, this is not the same $Q$ that it in B2jpg).$\\$ In your post 4 here, $E_2$ is missing the $\cos(\theta) =\frac{z}{(R^2+z^2)^{1/2} }$ factor.

 

[cookiemnstr510510]

Okay, I believe I see what you are saying-
E_ring= (kλ2pi2R₂z)/(2R₂² + z²)^(3/2)
and
E_Disk= (2pizQ)/((4piε₀(piR₂²-piR₁²)) [1/(z²+R₁²)^1/2-1/(z²+R₂²)^1/2]

Then I say E_Ring+E_Disk=0 and solve for lambda?
That seems like some really tedious algebra which I haven't tried yet. Wanted to know if this was the correct method before I try to do it.
Thanks!

 

[SammyS]

Okay, I believe I see what you are saying-
E_ring= (kλ2pi2R₂z)/(2R₂² + z²)^(3/2)
and
E_Disk= (2pizQ)/((4piε₀(piR₂²-piR₁²)) [1/(z²+R₁²)^1/2-1/(z²+R₂²)^1/2]

Then I say E_Ring+E_Disk=0 and solve for lambda?
That seems like some really tedious algebra which I haven't tried yet. Wanted to know if this was the correct method before I try to do it.
Thanks!

Quite a bit of that "cancels out" . You should either use Coulomb's coefficient, $\ k\$, for both or $\ \displaystyle \frac{1}{4\pi \varepsilon_0}\$. I suggest the latter. Gets rid of some $\ \pi \,$s .

You have: $\ \displaystyle E_{Ring} = \frac{kλ2\pi 2 R_2\, z} { \left( 2{R_2}^2 + z^2 \right)^{3/2}}\$ but I suppose you should be squaring (2R₂), not just the R₂ .

Changing to ε₀ form and the above correction gives:

$\ \displaystyle E_{Ring} = \frac{2\, \lambda \pi \, 2 R_2\, z} { 4\pi\,\varepsilon_0 \left( {(2R_2)}^2 + z^2 \right)^{3/2}}\$​

The expression for the disk is:
$\ \displaystyle E_{Disk} = \frac{2\pi z \,Q} {(4 \pi \varepsilon_0) \left(\pi {R_2}^2 - \pi {R_1}^2 \right)} \left(\frac{1}{( z^2 + {R_1}^2 )^{1/2} } - \frac{1}{(z^2 + {R_2}^2 )^{1/2} } \right)$
.

 

[cookiemnstr510510]

Okay! I’ll try it out! Thanks

 

[SammyS]

Okay! I’ll try it out! Thanks

I was editing that for a while. Just got finished.

 

[cookiemnstr510510]

okay so:
E ring= λz(2R₂/[2ε₀((2R₂)²+z²))^3/2
and
E washer= zQ/2ε₀(piR₂²-piR₁²) [1/√R₁²+z² - 1/√R₂²+z²]
then we say E ring=-E washer, solving for λ-
λ=-Q((2R₂)²+z²))^3/2/2R₂(piR₂²-piR₁²) [1/√R₁²+z² - 1/√R₂²+z²]

Im guessing no one wants to check my algebra LOL, just wanted to make sure this approach is correct, as long as my approach is correct my teacher is pretty lenient on algebraic mistakes with long calculations like this