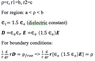Discussion Overview
The discussion revolves around the calculation of electric flux density in a coaxial cable, focusing on a specific homework problem. Participants explore the relevant equations and methods for solving the problem, including the application of boundary conditions and the implications of cylindrical symmetry.
Discussion Character
- Homework-related
- Technical explanation
- Debate/contested
Main Points Raised
- One participant expresses frustration over discrepancies between their solution and the book's answer, indicating a belief that they are using the correct equations.
- Another participant suggests using a specific differential equation related to radial electric flux density and emphasizes the importance of appropriate boundary conditions.
- A different participant notes that the problem exhibits cylindrical symmetry, which affects the expected relationships in the equations used.
- One participant requests clarification on their equation for the electric field and seeks examples to aid their understanding.
- Another participant advises solving the differential equation in general to find arbitrary constants, which should be determined using boundary conditions for each region of the coaxial cable.
- It is mentioned that the electric field outside the cable is zero and that the D field must be continuous across all regions.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correct approach or solution to the problem. Multiple competing views and methods are presented, and the discussion remains unresolved.
Contextual Notes
Some participants note the potential confusion arising from the use of similar symbols for different variables, which may complicate the discussion. There is also mention of the need for specific boundary conditions and the relationship between electric flux density (D) and electric field (E).