Electric potential energy in an infinite 2d crystal

AI Thread Summary
The discussion centers on calculating the electric potential energy in an infinite 2D crystal with alternating positive and negative charges. The formula presented involves a constant k as the distance r approaches infinity, with the potential energy expressed as We = k (±e0)(±e0)/(4 pi ε0 r). The challenge lies in summing an infinite number of terms, which theoretically converges to a final result. Participants reference the Madelung constant as a key component for this calculation, specifically seeking its value for a 2D arrangement. The conversation emphasizes the mathematical complexities involved in this theoretical framework.
Istvan
Messages
2
Reaction score
0
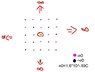
So.. we've got a 2D crystal, corresponding an infinite square net with +-e0 charges in each one (see the atached photo). Now I'd like to calculate the constant k..when r goes to infinity... We = k (+-e0)*(+-e0)/(4 pi eps0 r)..on the positive charge in the center caused by the negative and positive charges around him in the net. It's teoretically impossible to sum infinite number of terms, but the constant k will converge to the final result. So I'd like some help how to calculate that... thanks.
 

Attachments

  • untitled.JPG
    untitled.JPG
    15.1 KB · Views: 482
Last edited:
Physics news on Phys.org
'madelung constant' on wikipedia is a starting point
 
thanks

and what is the madelung constant for a 2d arrangement
 
Thread 'Motional EMF in Faraday disc, co-rotating magnet axial mean flux'

Thread 'Motional EMF in Faraday disc, co-rotating magnet axial mean flux'

So here is the motional EMF formula. Now I understand the standard Faraday paradox that an axis symmetric field source (like a speaker motor ring magnet) has a magnetic field that is frame invariant under rotation around axis of symmetry. The field is static whether you rotate the magnet or not. So far so good. What puzzles me is this , there is a term average magnetic flux or "azimuthal mean" , this term describes the average magnetic field through the area swept by the rotating Faraday...
View full post »

Similar threads

B E. Potential Energy: Uniformly Charged Hollow Sphere and Point Charge
Replies
4
Views
1K
I Computing the capacitance of a strange material
Replies
3
Views
730
B Definition of ground potential in infinite sheet charge distributions
Replies
11
Views
2K
I Potential difference between a battery's terminal and Earth ground
2
Replies
58
Views
4K
I Something about retarded potentials for oscillating electric dipole
Replies
1
Views
1K
Electric Potential Energy of Point Charge Systems
Replies
2
Views
870
Calculating the force on an electron from two positive point charges
Replies
2
Views
1K
I E-field around charged finite wire - intractable or not?
Replies
10
Views
899
Potential of a grounded conductor in the presence of an external charge
Replies
14
Views
3K
When Electric Field is 0 is potential also 0?
Replies
3
Views
5K

Hot Threads

Recent Insights

Back
Top