Electrical Field Theory and Tension In A String

[Jessehk]

Homework Statement

A ping-pong ball of mass 3.0 \times 10^{-15} is hanging from a light thread 1.0 m long, between two vertical parallel plates 10 cm apart, as shown. When the potential difference across the plates is 420 V, the ball comes to equilibrium 1.0 cm to one side of its original position.

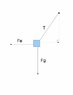
(See attached images for diagrams)




a) What is the electric field intensity between the plates?
b) What is the tension in the thread?
c) What is the magnitude of the electric force deflecting the ball?
d) What is the charge on the ball?

Homework Equations

\xi = \frac{v}{d}

F_e = \xi \cdot q

The Attempt at a Solution

First, I calculated the field strength between the two parallel plates.

\xi = \frac{420}{0.1} = 4200 N/C

Then, I drew the attached free body diagram, and from it, I got the following:

cos \theta = \frac{0.01}{1}

\theta \approx 89^{\circ{}}

Then sin(89) = \frac{mg}{T}

so T = 2.94 \times 10^{-3} N

(which is the right answer).

However, I'm lost when I try to do part C. Any answer that I get is nonsensical.
(The answer in the book is 2.94 \times 10^{-5} N)

I suspect that my FBD is not correct. I know that as soon as I know what Fe is, I can solve for the charge, q.
Did I also make a mistake in part A?

Any help would be greatly appreciated. If possible, It would be fantastic if somebody could point out the error in my thinking rather than just providing the solution. Thanks again.

 

[Doc Al]

However, I'm lost when I try to do part C. Any answer that I get is nonsensical.

Show what you did. Hint: Analyze horizontal force components. Your FBD looks fine--use it.

 

[Jessehk]

Thanks for the reply Doc Al :)

If you assume my FBD is correct, than it follows that the horizontal component of tension is equal to the electrical force.

Then: Fe = T \cdot cos(89^{\circ{}}) = 5.13 \times 10^{-5} N

Which isn't correct.

EDIT: I should also mention that the listed answer is only 2 sig.fig: 2.9 rather than 2.94. I assumed that it made no difference but it might indicate a mistake on my part...

 

[Doc Al]

Don't round off your angle to 89 degrees. You have the exact value of \cos\theta--use it.

 

[Jessehk]

Don't round off your angle to 89 degrees. You have the exact value of \cos\theta--use it.

*SLAPS HEAD*

Thanks Doc Al. This is the second time that you've helped me; I'm really grateful.
That's a testament to the importance of not rounding too early.

 

[Doc Al]

I know the feeling. I've slapped my head--and banged it against walls--so many times it's a wonder that I can feed myself.

And you're welcome.