Bromio
- 59
- 0
Hi.
Sorry my spelling, because I am not English.
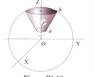
In a sphere truncated sector with an angle of 60 degrees, there is a uniform charge distribution, \rho. Calculate the electric field in (0,0,0). The sector starts in z=a and ends in z = b. The sphere center is in (0,0,0).
To calculate the electric field, I use:
\bar{E}(\bar{R}) = \displaystyle\frac{1}{4 \pi \epsilon_0} \displaystyle\int\displaystyle\int\displaystyle\int_{V'} \rho\left(\bar{R}\right) \displaystyle\frac{\bar{R}-\bar{R}'}{\left|\bar{R}-\bar{R}'\right|^3}\;dV'
I know that:
\rho\left(\bar{R}\right) = \rho
\bar{R} = 0
\bar{R}' = \hat{R}'R'
dV' = R'^2\sin\theta\;dRd\theta d\phi
Now, I substitute these values in the integral and I solve it.
What is the problem? I don't know if I can integrate using cylindrical coordinates directly or, on the other hand, if I must use rectangular coordinates:
\bar{E}(0) = \displaystyle\frac{1}{4 \pi \epsilon_0} \displaystyle\int_0^{2 \pi}\displaystyle\int_0^{\pi /6}\displaystyle\int_a^b \rho\displaystyle\frac{\hat{R}R'}{R'^3}R'^2 \sin \theta\;dRd\theta d\phi
or
\bar{E}(0) = \displaystyle\frac{1}{4 \pi \epsilon_0} \displaystyle\int_0^{2 \pi}\displaystyle\int_0^{\pi /6}\displaystyle\int_a^b \rho\displaystyle\frac{-\hat{z}R' \cos \theta}{R'^3}R'^2 \sin \theta\;dRd\theta d\phi ?
In first situation, the result will depend on \hat{R}, but, in the second one, it will depend on \hat{z}. Which is the correct solution and why?
Thank you.
Bromio.
Sorry my spelling, because I am not English.
Homework Statement
In a sphere truncated sector with an angle of 60 degrees, there is a uniform charge distribution, \rho. Calculate the electric field in (0,0,0). The sector starts in z=a and ends in z = b. The sphere center is in (0,0,0).
Homework Equations
To calculate the electric field, I use:
\bar{E}(\bar{R}) = \displaystyle\frac{1}{4 \pi \epsilon_0} \displaystyle\int\displaystyle\int\displaystyle\int_{V'} \rho\left(\bar{R}\right) \displaystyle\frac{\bar{R}-\bar{R}'}{\left|\bar{R}-\bar{R}'\right|^3}\;dV'
The Attempt at a Solution
I know that:
\rho\left(\bar{R}\right) = \rho
\bar{R} = 0
\bar{R}' = \hat{R}'R'
dV' = R'^2\sin\theta\;dRd\theta d\phi
Now, I substitute these values in the integral and I solve it.
What is the problem? I don't know if I can integrate using cylindrical coordinates directly or, on the other hand, if I must use rectangular coordinates:
\bar{E}(0) = \displaystyle\frac{1}{4 \pi \epsilon_0} \displaystyle\int_0^{2 \pi}\displaystyle\int_0^{\pi /6}\displaystyle\int_a^b \rho\displaystyle\frac{\hat{R}R'}{R'^3}R'^2 \sin \theta\;dRd\theta d\phi
or
\bar{E}(0) = \displaystyle\frac{1}{4 \pi \epsilon_0} \displaystyle\int_0^{2 \pi}\displaystyle\int_0^{\pi /6}\displaystyle\int_a^b \rho\displaystyle\frac{-\hat{z}R' \cos \theta}{R'^3}R'^2 \sin \theta\;dRd\theta d\phi ?
In first situation, the result will depend on \hat{R}, but, in the second one, it will depend on \hat{z}. Which is the correct solution and why?
Thank you.
Bromio.
Last edited: