PrashntS
- 25
- 0
1. The question is to find the volume charge density. Given is non uniform, but spherically symmetric electric field, E=K.r4, K being a constant. Original question can be viewed in image:

* Question no. 53
Answer is: ρ=6Kr3ε
Tried solving so many times. Once, I got half the answer I should have got!
Solution steps are attached.:
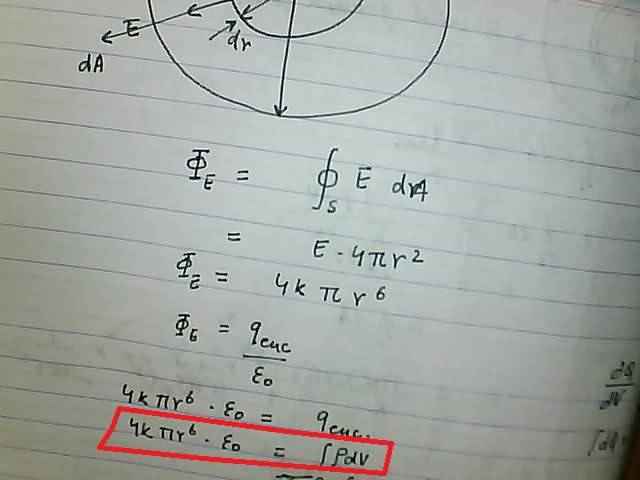
I got struck at the last equation,:
4Kεπr6=∫ ρ.dV
* Question no. 53
Homework Equations
Answer is: ρ=6Kr3ε
The Attempt at a Solution
Tried solving so many times. Once, I got half the answer I should have got!
Solution steps are attached.:
I got struck at the last equation,:
4Kεπr6=∫ ρ.dV