- 23,198
- 7,671
Homework Statement
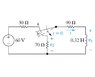
In the circuit shown in (Figure 1) , the switch makes contact with position b just before breaking contact with position a. As already mentioned, this is known as a make-before-break switch and is designed so that the switch does not interrupt the current in an inductive circuit. The interval of time between "making" and "breaking" is assumed to be negligible. The switch has been in the a position for a long time. At t = 0 the switch is thrown from position a to position b.
What percentage of the initial energy stored in the inductor is dissipated in the 90 Ω resistor 1.4 ms after the switch is thrown from position a to position b?
Figure 1:
Homework Equations
##i(t) = 0.5e^{-500t}##
##i(0) = 0.5 A##
##p(t) = i(t)^2R##
##W_i=\frac{1}{2}LI^2##
The Attempt at a Solution
I found the equation for the current after ##t≥0##. To find the power dissipated in the 90 ohm resistor, I thought I was supposed to find the integral of the power from 0 to 1.4 ms.
Initial energy is ##W_i = (0.5)(0.32)(0.5^2) = 0.04375 J##
Power is:
##p(t) = i(t)^2R##
##p(t) = (0.5e^{-500t})^2(90) = 22.5e^{-1000t}##
The integral of power is: ##\int_0^{1.4ms} 22.5e^{-1000t}\, dt = 22.5 \int_0^{1.4ms} e^{-1000t}\, dt = \left. \frac{-22.5}{1000}(e^{-1000t}) \right|_0^{0.0014} = -0.0225(e^{-1.4}-e^0) = -0.0225(-0.7534) = .01695 J##
##W(1.4ms) = 0.01695 J##
The percentage of initial energy is: ##\frac{0.01695}{0.04375}(100) = 38.75##
Unfortunately it appears that answer is incorrect. Any ideas where I might have gone wrong?