- #1
Spinnor
Gold Member
- 2,216
- 430
Picture a charging capactor, you know the E field, and the induced B field, the energy flow is just EXB.
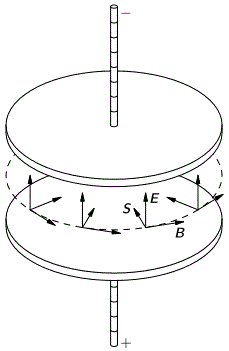
Please describe for me in rough terms the energy flow vector field near and far from the slowly charging capacitor? The flow of energy must ultimately come from the source of energy that charges the capacitor, say a battery? Has anyone ever seen an image of such a flow of energy for this system? Can you roughly sketch what it should look like? Do you simply draw lines of S from the battery to the entrance of the gap of the capacitor? Let the only resistance of the circuit be the internal resistance of the battery. Feynman goes into this here,
http://www.feynmanlectures.caltech.edu/II_27.html
Thanks!
Edit, where in space and time can one safely say that the field S should be zero?
Please describe for me in rough terms the energy flow vector field near and far from the slowly charging capacitor? The flow of energy must ultimately come from the source of energy that charges the capacitor, say a battery? Has anyone ever seen an image of such a flow of energy for this system? Can you roughly sketch what it should look like? Do you simply draw lines of S from the battery to the entrance of the gap of the capacitor? Let the only resistance of the circuit be the internal resistance of the battery. Feynman goes into this here,
http://www.feynmanlectures.caltech.edu/II_27.html
Thanks!
Edit, where in space and time can one safely say that the field S should be zero?
Last edited: