Saptarshi Sarkar
- 98
- 13
- Homework Statement
- A particle moves in a circular orbit about the origin under action of a central force ##\vec F = -k\hat r/r^3##. If the potential energy is zero at infinity, what is the total energy of the particle?
- Relevant Equations
- ##E_{total} = E_{kinetic} + E_{potential}##
I calculated the potential energy of the particle as follows :
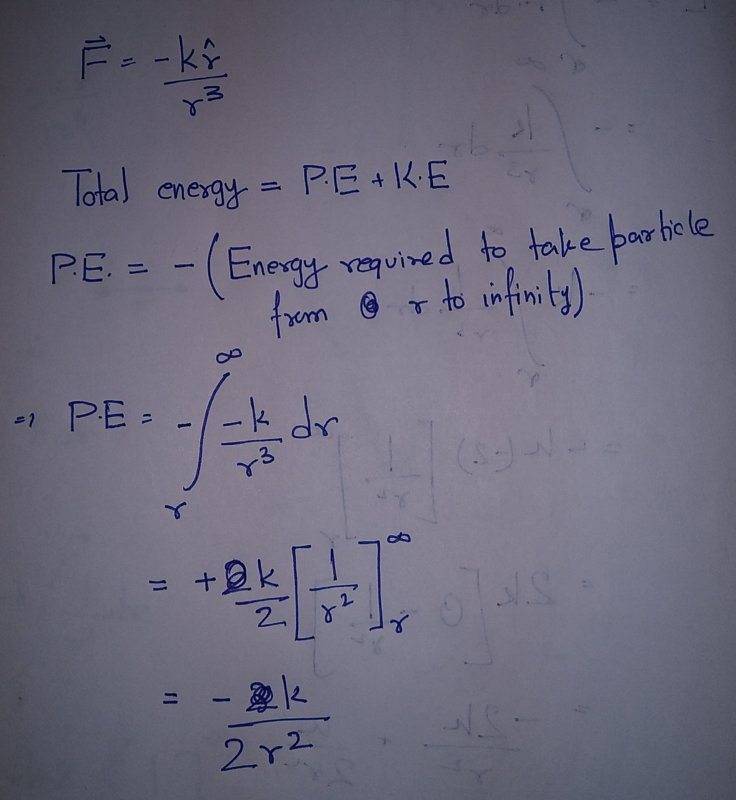
But I am not sure how to calculate the kinetic energy. I know that if it was a satellite orbiting a Earth, I could use ##\frac {GMm} {r^2} = \frac {mv^2} {r}## to calculate the velocity v and they I could calculate kinetic energy as ##E_{kinetic} = \frac {mv^2} 2##.
But how do I calculate the velocity for the given force?
But I am not sure how to calculate the kinetic energy. I know that if it was a satellite orbiting a Earth, I could use ##\frac {GMm} {r^2} = \frac {mv^2} {r}## to calculate the velocity v and they I could calculate kinetic energy as ##E_{kinetic} = \frac {mv^2} 2##.
But how do I calculate the velocity for the given force?