NotanEngineer
- 2
- 0
Homework Statement
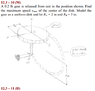
A 0.2 lb gear is released from rest in the position shown (Okay so this essentially a circular gear in the groves on an adjacent wall that is also circular. Think perpendicular circles with different radii. The gear is a circle, and the gear teeth are in a circular pattern; the picture is attached) Find the maximum speed of the center of the disk and let the radius of the gear be 2 inches. And the radius of the path is 3 inches.
Homework Equations
2nd energy Principle: E1= V1 +T_t1 + T_r1 = E2 = V2 + T_t2 + T_r2
V= mgh T_t= 1/2mv^2 T_r= 1/2 ω\bullet [Ic] \omega
The Attempt at a Solution
My attempt was to treat the path around the wall as translational, and keep the disk spinning around the center as rotational energy. The problem I'm having is I don't really know how to configure my omega or the moments of inertia. I think my biggest issue is setting the coordinate system, and defining all of the parts that go into the equations that will eventually be put into my relevant energy equations.