Engineer a Waterski Contraption - Physics Forums

[blevinstein]

I am a waterskiier and have been thinking about trying to engineer a... "contraption" which will ride on top of the water similar to a water skier on a ski. In order to get an idea of the scale of this project though, I first need a basic understanding of the forces that allow a skier to stay on top of the water.

I found an excellent previous discussion of this already on these forums:

https://www.physicsforums.com/showthread.php?t=16018

but the basic consensus seems to be that complicated physics models are necessary to even approximate how it works. Foolishly, I've tried to model a skier in as simple a fashion as I can, but my model seems to give me terribly inaccurate results. Anyways, I've done some rough sketches in MS paint of how I would imagine it could be modeled, and would appreciate any input on why this model is so far off of reality.

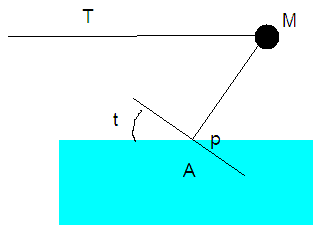
(see skier.png, attached)

this is how I would imagine the skier in as simple of a reality as I can - water, ski, and a mass representing the skier. T is tension, M is the mass of the skier, A is the surface area of the part of the ski which is underwater, and t and p are supposed to be theta and phi (so they represent arbitrary angles).

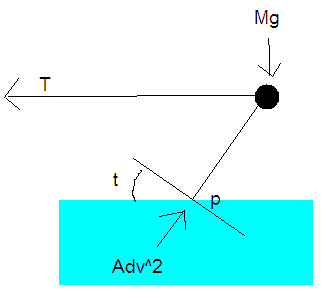
(see forces.png, attached)

now, these are the forces that are acting on my skier. T is tension on the rope, Mg is the weight of the skier, and the most confusing is Adv^2. As Chi Meson explained in the previous waterskiing thread, because I want to approximate the mass of water hitting the ski at a given time (m/t) I use surface area (d^2) x velocity (d/t) x density of water (m/d^3) which gives me m/t and then I multiply by velocity again to get mv/t, which is a unit of force. so, A is surface area, d is density of water, and v is velocity, so the force is Adv^2, and I approximate it to be perpendicular to the water ski.

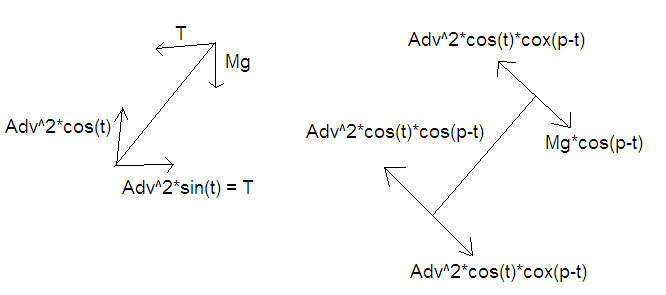
(see forces2.png, attached)

finally, I break the forces involved down into component form and examine the net forces. I have 2 diagrams here; the first is the linear forces and the second is the rotational forces which result from the linear forces. The linear diagram is pretty straightforward - Adv^2 is split based on theta into vertical and horizontal components. the tension on the rope has to be equal to the horizontal force so that the skier stays in place. and Mg is the weight of the skier, as before. The rotational forces are much more complicated. phi-theta (p-t) is, if you look at the first image, the angle between the skier and the water. so, we again split Adv^2*cos and Adv^2*sin into 2 vectors each, one which is compressing the skier and one which is rotating the skier by multiplying by the sin and cos of phi minus theta (p-t). We know that T is equal to Adv^2*sin(t), yielding the same rotational force. And finally, as with the components of Adv^2, we ignore the force compressing the skier and end up with Mg*cos(p-t). Any forces not accounted for here are lost because they are applied vertically along the skier - that is, the ski is being pushed up towards the skier or the skier is being pulled down towards the ski, which I don't allow to happen.

(note: sorry, in some places I accidentally typed "cox" instead of "cos" and I know this is getting way too long so I'll try to wrap it up)

ok, so finally, I want to know the strength of the forces pushing the skier up and rotating the skier.

for the vertical force problem, we simply look at the linear force diagram and get:

Adv^2*cos(t)-Mg

which is a force, so by dividing by M, we get the vertical acceleration of the skier at this point in time (which, if the skier is stable, should be 0)

and for the rotational force problem, we just add up the vectors in the rotational force diagram: (clarification: I am calculating the acceleration of theta, which is correlated to the rotation of the skier)

Adv^2*cos(t)*cos(p-t) + Mg*cos(p-t) - 2Adv^2*sin(t)*sin(p-t)

and by dividing by M times the mean distance (by mass) of a point on the skier from the center of gravity of the skier (which gives us the rotation in... circumferences?). (we can tell that this is necessary because dividing the force by M gives us an acceleration through distance, but rotation is not distance, it is unitless)

I can share some obviously wrong calculations if it is necessary, but before I do so, is there anything obviously wrong about my model aside from the simplifications and assumptions I made to make it fit into 2 dimensions in such a simple fashion?

Thank you very much in advance,
Brian Levinstein

 

[blevinstein]

I think my rotational forces are completely wrong. I don't know how the distance from where a force is applied to the center of mass on the skier affects the rotation, and this rotation affects my vertical force/acceleration calculations because the rotation is around the center of mass of the skier, not around the area where the ski contacts the water, and therefore applies a force I haven't accounted for.

UPDATE: I figured out that the acceration of theta, as I calculated it, does not give you rotation in circumferences, it gives you rotation in radians

UPDATE: okay, now I think I have the rotation figured out. If Ft is the force applied to change theta (i.e. rotate the skier) and At is the acceleration of theta, what I said before is:

Ft = Adv^2*cos(t)*cos(p-t) + Mg*cos(p-t) - 2Adv^2*sin(t)*sin(p-t)
At = Ft / M * c

where c is the mean distance, by mass, of any point on the skier from the center of mass of the skier, and At is in radians.

I'm not sure if this is correct, but now I thought maybe I could apply this rotational force at the point where the ski touches the water. Working backwards, the force we are applying is equal to At * M * b, where b is the distance from the ski to the center of mass of the skier. If you work it out (and this is just too complicated to do a mspaint drawing of) the forces end up being applied like this:

horizontal force Fx = At*M*b*sin(p+t)
vertical force Fy = At*M*b*cos(p+t)

Now that I think about it I don't think this is correct because adding another linear force would again affect the rotational forces, so I don't think I can add this into the equations.

I do seem to be missing some forces, though. I calculated, for example, that a 70 kg (150 lb) skier going 10 m/s (22mph) with the ski at a 30 degree angle to the water and the skier perpendicular to the ski, the surface area of the ski in contact with the water can be as little as 80 square centimeters and it would hold the skier above the water. This is obviously not correct as this is about 12 square inches, and it definitely is not possible for me to ski on a classroom ruler. =D

UPDATE:

At = Ft / M * c

nevermidn this is not correct, instead of dividing by c each force should be divided by the distance between the point at which it is applied and the center of mass, then they should be totalled and divided by M

so, I think this is a more accurate version of my forces diagrams:

tension T and the force of gravity Mg are both applied to the center of mass of the skier (note: tension might not be applied at the center of mass, but for now I'll assume it is) so neither will rotate the skier. Also, b is the distance from the center of mass of the skier to the ski, and I show that the rotational force is divided by b, and it will then be divided by M to give At

 

[blevinstein]

no, this doesn't make any sense; the amount of force applied is not dependent on where it is applied. it does make sense, however, that T and Mg do not cause rotation.

Ft = Adv^2cos(t)cos(p-t) - Adv^2sin(t)sin(p-t)
Ft = Adv^2(cos(t)cos(p-t) - sin(t)sin(p-t))
Ft = Adv^2cos(t+p-t)
Ft = Adv^2cos(p)

however, I think that I have a new problem because phi is the angle between the ski and skier as I drew it, but really, it should be the angle between the ski and a line which goes from the center of the area of the ski which is underwater to the center of mass of the skier, so phi will not remain constant if the ski moves vertically (and more or less of the ski is underwater)

This means that, for example, if the skier is balanced in the middle of the underwater portion of the ski at a 90 degree angle to the ski, because the water applies force perpendicular to the ski, the ski will never rotate. It seems to me that this makes sense. Any thoughts? (excluding, of course, water friction, air friction, etc)