Engineering Mechanics - Statics

[cordines]

Homework Statement

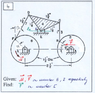
Please refer to the attached diagram. I am trying to find the unknown load F (along line of action l_F) that will keep the system in equilibrium as well as compute all reaction forces developed at the joints.

Homework Equations

Summation of forces in the horizontal and vertical direction as well as moments about a point.

The Attempt at a Solution

I have split the mechanism into these members:

Member AB, Member BC, Member CDE, Member DF and Member FG as well as the slider. From these members I can derive the following equations. For:

Member AB - 3 equations (summation of forces in horizontal and vertical direction and moments)
Member BC - 3 equations
Member CDE - 3 equations
Member DF - 3 equations
Member FG - 3 equations
Slider E - 2 equations (summation of forces in horizontal and vertical direction)

Total number of equations = 17.

However I have 16 unknown parameters which are:

Joint A (A_x, A_y)
Joint B (B_x, B_y)
Joint C (C_x, C_y)
Joint D (D_x, D^y)
Joint E (E_x, E_y)
Joint F (F_x, F_y)
Joint G (G_x, G_y)
Unknown force F (along line of action l_F)
Slider reaction S_y

Clearly I need the same number of Unknown parameters and equations to solve. What am I doing wrong?

 

[pongo38]

"the unknown load F (along line of action lF)" baffles me because on the diagram they are parallel but separated. Is the diagram correct? An additional comment is that, although your attempt is well meant, it is not necessarily the best way to approach the problem because with so many unknowns there is a very high chance of making mistakes. For example, member 3, by inspection carries no moment or shear force; only an axial force. So you could look for simplification before assembling a lot of trivial equations. You can also recognise that joints C and D are hinges. Therefore the moments on one side of those joints must sum to zero... and I believe you could find other simplifications that either reduce the unknowns or at least reveal them gradually through the calculation process, rather than lumpthem into an impractical matrix of equations.

 

[nvn]

Could you throw out one equation, and then solve for the 16 unknowns?

 

[cordines]

@pongo38. Note that the moment and force in red are both given. What exactly do you mean by "the unknown load F (along line of action lF)" are parallel but separated"?

@nvn. Yes, I threw out one equation and solved 15 equations with 15 unknowns and then used the other equation as a check to see if the LHS matches the RHS. However, that didn't happen.

 

[pongo38]

What I mean is: On the wheel labelled 'A' there is a red F with 2 arrows. Presumably the upper arrow is the symbol that F is a vector, and the lower arrow indicates its line of action, whose position is not well defined. Then you have LF at point E. Is the red F supposed to be acting through point E, or point A, or some other point? Sorry to be difficult, but it's not clear to me. Concerning your remark to nvn, if the system is statically determinate, then, in general there will be a spare equation you can use for checking.

 

[cordines]

No, on wheel A there is only one horizontal force (which is taken to the left). This force acts at the midspan of the member AB as denoted by the parameter r/2. The arrow on the force F indicates that it is a vector. The arrow below the force F indicates how it acts and its direction.

The force acting through the line of action lF is taken to act at point E.

I agree that the problem is not clear but that was how it was assigned.