Entropy in Information theory vs thermodynamic

[Angella]

We Now From Information Theory That Entropy Of Functions Of A Random Variable X Is Less Than Or Equal To The Entropy Of X.

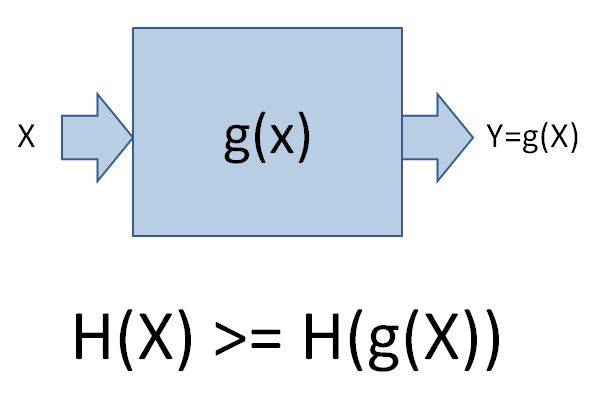
Does It Break The Second Law Of Thermodynamic?

 

[paulfr]

Unless you add energy to a system, its Entropy will increase.
So you have it backwards
H[g(x)] > H(x)
Entropy is a measure of disorder which usually increases
unless work is being done or energy is being added.

 

[DrZoidberg]

That law only applies if x is the only argument of that function.
Let's assume x is the state of the universe and g is the laws of physics applied over a specific amount of time. Then g(x) will be the future state of the universe.
However the increase in entropy happens because of quantum randomness, that means our function g needs a second argument R which is a source of randomness. So you then have g(x, R).
That's if x is the state you measure with some instruments i.e. a classical state.
If on the other hand you look at a pure quantum system without any measurements or wave function collapse then there is no randomness and you just have g(x). But in such a case there is also no change in entropy/information. Conservation of information is a basic law of quantum mechanics.

 

[Angella]

That law only applies if x is the only argument of that function.
Let's assume x is the state of the universe and g is the laws of physics applied over a specific amount of time. Then g(x) will be the future state of the universe.
However the increase in entropy happens because of quantum randomness, that means our function g needs a second argument R which is a source of randomness. So you then have g(x, R).
That's if x is the state you measure with some instruments i.e. a classical state.
If on the other hand you look at a pure quantum system without any measurements or wave function collapse then there is no randomness and you just have g(x). But in such a case there is also no change in entropy/information. Conservation of information is a basic law of quantum mechanics.

thanks a lot DrZoidberg, but i still have a bit ambiguity.

do you mean that second law applies only in situations that our function have more than one argument? because in the data processing inequality g has just one argument and we see that the second law is not applied!

and can please explain more about R and what is the source of randomness?

and why quantum randomness cause an increase in entropy?

thank you again

 

[DrZoidberg]

Actually my previous answer was not completely correct. Of course the entropy law in information also works for more than one argument. But if you have two arguments then you have to look at the combined entropy of both.
So H(x, R) >= H(g(x, R)).
However even if there was no randomness in physics the 2nd law of thermodynamics would probably still be there because the definition of entropy in physics is different from the one in information theory. In physics the entropy/information content of a system is the log of the number of possible states that have the same macroscopic description. Which is of course kind of arbitrary since any physicist can decide what qualifies as macroscopic in any particular case.
That means it's possible for entropy in a physical system to increase even if from an information theory point of view it is staying constant.