MHB Equality of Angles: 3 Equal Angles in a Picture
- Thread starter Drain Brain
- Start date
-
- Tags
- Angles
Click For Summary
SUMMARY
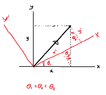
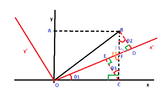
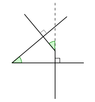
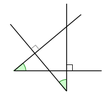
The discussion centers on the equality of three angles in a geometric configuration, specifically utilizing the properties of vertical angles and the sum of angles in triangles. It establishes that angles $\hat{F_1}$ and $\hat{F_2}$ are equal due to their vertical relationship, leading to the conclusion that $\theta_1$, $\theta_2$, and $\theta_3$ are all equal. The theorem stating that two angles with mutually perpendicular sides are equal is also highlighted, emphasizing its relevance in both geometry and physics, particularly in problems involving inclined planes.
PREREQUISITES- Understanding of vertical angles and their properties
- Knowledge of triangle angle sum theorem
- Familiarity with mutually perpendicular lines
- Basic concepts of geometry applicable to physics
- Study the properties of vertical angles in depth
- Explore the triangle angle sum theorem with practical examples
- Investigate the application of mutually perpendicular angles in physics problems
- Learn about inclined planes and their geometric implications
Students of geometry, physics enthusiasts, and educators looking to deepen their understanding of angle relationships and their applications in real-world scenarios.
Similar threads
- · Replies 10 ·
- · Replies 1 ·
- · Replies 4 ·
- · Replies 17 ·
- · Replies 2 ·
High School
Understanding the Pythagorean Theorem
- · Replies 38 ·
- · Replies 7 ·
- · Replies 6 ·
- · Replies 4 ·
- · Replies 1 ·