You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
MHB Equality of Angles: 3 Equal Angles in a Picture
- Thread starter Drain Brain
- Start date
-
- Tags
- Angles
AI Thread Summary
The discussion centers on the equality of three angles in a geometric configuration, demonstrating that they are equal due to the properties of triangles and vertical angles. It explains that the sum of angles in a triangle is 180 degrees, leading to the conclusion that angles θ2 and θ3 are equal based on their relationships with vertical angles and right angles. The theorem stating that angles with mutually perpendicular sides are equal is highlighted as a key principle in this explanation. Additionally, the concept is noted for its practical applications in physics, particularly in problems involving inclined planes. Understanding these geometric relationships is essential for solving related mathematical and physical problems.
Mathematics news on Phys.org
Evgeny.Makarov
Gold Member
MHB
- 2,434
- 4
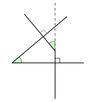
There is a theorem saying that two angles whose sides are mutually perpendicular are equal.
mathmari
Gold Member
MHB
- 4,984
- 7
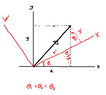
View attachment 2891Drain Brain said:Can you explain why the 3 angles in the picture are the same.
The sum of the angles of a triangle is equal to $180$.
The angles $\hat{F_1}$ and $\hat{F_2}$ are a pair of vertical angles, so they are equal, $\hat{F_1}=\hat{F_2}$
At the triangle $BFD$, the sum of the angles is:
$$\theta_2+\hat{F_2}+90 ^{\circ}=180^{\circ} \Rightarrow \theta_2+\hat{F_2}=90^{\circ} \ \ \ (1)$$
At the triangle $CEF$, the sum of the angles is:
$$\theta_3+\hat{F_1}+90^{\circ}=180 \Rightarrow \theta_3+\hat{F_1}=90^{\circ} \ \ \ (2)$$
$$\xrightarrow[(1)]{(2)} \theta_2+\hat{F_2}=\theta_3+\hat{F_1} \Rightarrow \theta_2=\theta_3$$
Then we do the same for the triangles $OFC$ and $BDF$ and we conclude that $\theta_1=\theta_2=\theta_3$
Attachments
bergausstein
- 191
- 0
Evgeny.Makarov said:There is a theorem saying that two angles whose sides are mutually perpendicular are equal.
what do you mean? Can you show me a picture of mutually perpendicular angles? please bear with me. :) thanks!
Evgeny.Makarov
Gold Member
MHB
- 2,434
- 4
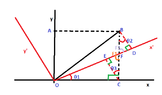
I mean the following situation.
View attachment 2923
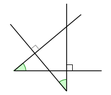
If you consider angles composed of two rays (semi-lines) rather than lines infinite in both directions, then the angles may add up to $180^\circ$. But if you have two pairs of lines: $l_1,l_2$ and $l_1',l_2'$ such that $l_1\perp l_1'$ and $l_2\perp l_2'$ and if you consider the smaller angles formed by these lines, then these angles are equal.
View attachment 2922
This property is especially useful in physics for solving problems with inclined plane.
View attachment 2923
If you consider angles composed of two rays (semi-lines) rather than lines infinite in both directions, then the angles may add up to $180^\circ$. But if you have two pairs of lines: $l_1,l_2$ and $l_1',l_2'$ such that $l_1\perp l_1'$ and $l_2\perp l_2'$ and if you consider the smaller angles formed by these lines, then these angles are equal.
View attachment 2922
This property is especially useful in physics for solving problems with inclined plane.
Attachments
Hi,
I was watching the following video. I found some points confusing. Could you please help me to understand the gaps? Thanks, in advance!
Question 1:
Around 4:22, the video says the following.
So for those mathematicians, negative numbers didn't exist. You could subtract, that is find the difference between two positive quantities, but you couldn't have a negative answer or negative coefficients. Mathematicians were so averse to negative numbers that there was no single quadratic...
Insights auto threads is broken atm, so I'm manually creating these for new Insight articles.
In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra
Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/
by...
Suppose ,instead of the usual x,y coordinate system with an I basis vector along the x -axis and a corresponding j basis vector along the y-axis we instead have a different pair of basis vectors ,call them e and f along their respective axes.
I have seen that this is an important subject in maths
My question is what physical applications does such a model apply to?
I am asking here because I have devoted quite a lot of time in the past to understanding convectors and the dual...
Similar threads
- Replies
- 10
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 4
- Views
- 2K
- Replies
- 17
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 38
- Views
- 4K
- Replies
- 7
- Views
- 2K
- Replies
- 6
- Views
- 1K
- Replies
- 4
- Views
- 1K
- Replies
- 1
- Views
- 2K
Hot Threads
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math
-
B What could prove this wrong? I'm having a dispute with friends
- Started by ducknumerouno
- Replies: 94
- General Math
-
B About a definition: What is the number of terms of a polynomial P(x)?
- Started by littlemathquark
- Replies: 48
- General Math
-
B How Many Straight Lines to Connect an N by M Array of Points in a Closed Loop?
- Started by bob012345
- Replies: 25
- General Math
-
B Geometry Puzzle with 20 points in a cross pattern
- Started by bob012345
- Replies: 31
- General Math
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math