Samzor123
- 1
- 0
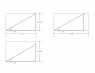
A few days ago I got really excited when I found the equation for a retangles radius (distance from its center to its perimeter given an angle)
I have no idea if this is something very simple and stupid but my math teacher said it was impressive, I'm still in high school
It's like this:
(w/2)*sqrt(cos^2(theta)) + (h/2)*sqrt(sin^2(theta))
(Or my attempt at latex):
\frac{w}{2}\sqrt{cos^{2}(\theta)} + \frac{h}{2}\sqrt{sin^{2}(\theta)}
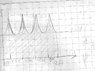
gives the length of the line from the center of a rectangle (width w, height h) to its perimeter at angle of theta.
I graphed it also with x = theta (radians), for a rectangle of width 1 and height 1:
http://dl.dropbox.com/u/1828729/rr/graph.png (it's a big image)
I needed to share this, excuse me if it's ridiculously simple.
I have no idea if this is something very simple and stupid but my math teacher said it was impressive, I'm still in high school
It's like this:
(w/2)*sqrt(cos^2(theta)) + (h/2)*sqrt(sin^2(theta))
(Or my attempt at latex):
\frac{w}{2}\sqrt{cos^{2}(\theta)} + \frac{h}{2}\sqrt{sin^{2}(\theta)}
gives the length of the line from the center of a rectangle (width w, height h) to its perimeter at angle of theta.
I graphed it also with x = theta (radians), for a rectangle of width 1 and height 1:
http://dl.dropbox.com/u/1828729/rr/graph.png (it's a big image)
I needed to share this, excuse me if it's ridiculously simple.
Last edited by a moderator: