ps098
- 2
- 0
Hi everyone, this will probably be very easy for someone but I'm really struggling to get this to work. I have experimental data whose baseline and peak midpoints I have fitted tangents to, and I have found the points where they intersect. I now want to find the red line which bisects these two tangents, but whatever I do the plot comes out at completely the wrong angle. I have included an example, with my beautiful handwritten workings (lol).
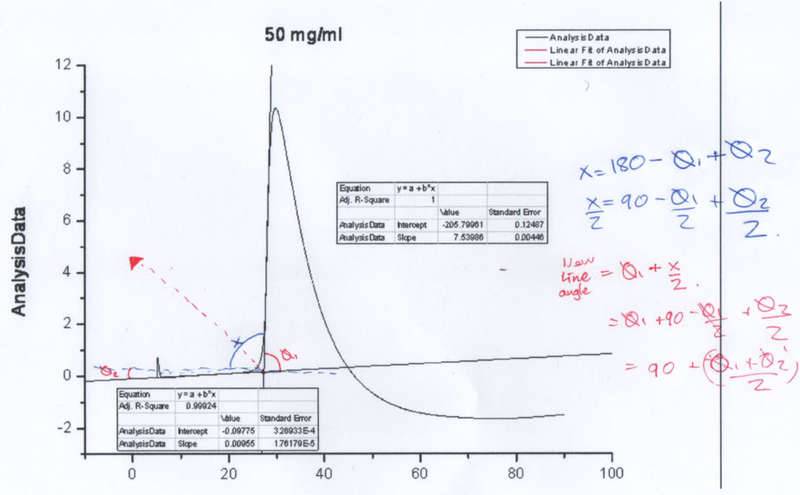
If anyone can help, I'd really appreaciate it, my MSc will be all the better for it :D
Cheers
If anyone can help, I'd really appreaciate it, my MSc will be all the better for it :D
Cheers