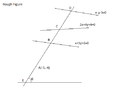
Let equation of line \(AC\) be
\[\frac{y+4}{\sin \theta}=\frac{x+5}{\cos \theta}=r\]
Let line \(AE\) make angle \(\theta\) with the \(x\)-axis and intersects \(x+3y+2=0\) at \(B\) at a distance \(r_1\) and line \(2x+y+4=0\) at \(C\) at a distance \(r_2\) and line \(x-y-5=0\) at \(D\) at a distance \(r_3\).
\[\therefore \ AB=r_1 , \ AC=r_2, \ AD=r_3\]
Putting \(x=r_1\cos \theta -5\) and \(y=r_1\sin \theta -4\) in \(x+3y+2 =0\) we get
\[\begin{aligned}
x+3y+2 &=0 \\
\Rightarrow r_1 \cos \theta -4 +3(r_1 \sin \theta -4)+2 &=0 \\
\Rightarrow r_1 &= \frac{-5-3(4)+2}{\cos \theta +3 \sin \theta} \\
\Rightarrow r_1 &= \frac{15}{\cos \theta +3 \sin \theta} \quad \cdots \text{(i)}
\end{aligned}\]
Similarly,
\[\begin{aligned}
r_2 &= \frac{10}{2\cos \theta + \sin \theta} \quad \cdots \text{(ii})\\
r_3 &= \frac{6}{\cos \theta - \sin \theta} \quad \cdots \text{(iii)}
\end{aligned}\]
But it is given that
\[\begin{aligned} \left(\frac{15}{AB}\right)^2 + \left(\frac{10}{AC}\right)^2 &= \left(\frac{6}{AD}\right)^2 \\ \Rightarrow \left(\frac{15}{r_1}\right)^2 + \left(\frac{10}{r_2}\right)^2 &= \left(\frac{6}{r_3}\right)^2 \\ \Rightarrow (\cos \theta + 3\sin \theta )^2+(2\cos \theta + \sin \theta)^2 &=(\cos \theta -\sin \theta)^2 \quad [\text{from equations (i), (ii) and (iii)}] \\ 4\cos^2 \theta + 6 \sin ^2 \theta +12 \sin \theta \cos \theta &=0 \\ (2\cos \theta + 3 \sin \theta )^2 &=0 \\ 2\cos \theta + 3 \sin \theta &=0 \\ \tan \theta &=-\frac{2}{3}\end{aligned}\]
On substituting this in the equation of \(AC\), we get
\[y+4=(x+5)\tan \theta \\ \Rightarrow y+4=-\frac{2}{3}(x+5) \\ \Rightarrow 2x+3y+22=0\]