- #1
NEGATIVE_40
- 23
- 0
hey guys, I have a question regarding how to get the potential energy for this. I can get the correct answer, but the solutions do a step that makes absolutely no sense to me, so hopefully someone leads me in the right direction 
Using energy method,
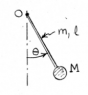
derive the equation of motion for the pendulum which consists of the slender uniform rod of mass m and the bob of mass M. assume small oscillations, and neglect the radius of the bob.
***see attachment for diagram***
[tex] I_o = \frac{1}{3}mL^2 + ML^2 [/tex] is the moment of inertia
[tex] V = mgh [/tex]
is the gravitational potential energy
[tex] T = \frac{1}{2}I_o \omega^2 = \frac{1}{2}I_o \dot{\theta}^2 [/tex]
is the kinetic energy
[tex] \frac{d}{dt}(T+V)=0 [/tex]
to get equation of motion
My expression for V is this;
[tex] V = -mg\frac{L}{2}cos(\theta)-MgLcos(\theta) [/tex]
where I have taken the datum as being at the pivot acting postive up. This is different to the solution, which has written[tex] V_{solution} = mg\frac{L}{2}(1-cos(\theta))+ MgL(1-cos(\theta)) [/tex]
I don't understand why they have 1 - cos(theta). Wouldn't you just want the cosine of the angle?
Anyway, if I continue to the derivtive step (doing the small angle approximation), this doesn't seem to have an effect. So...
[tex] \frac{d}{dt}(T+V)=\frac{d}{dt}\left ( \frac{1}{2}(M+\frac{m}{3})L^2\dot{\theta}^2 -mg\frac{L}{2}cos(\theta)-MgLcos(\theta)\right ) =0 [/tex]
which yields, after a lot of manipulation,
[tex] \ddot{\theta}+\frac{3g(m+2M)}{2L(m+3M)}\theta = 0 [/tex]
which is what the textbook says is correct.
is the textbooks expression for the potential energy wrong in this case? or did I get lucky in getting the right answer? It doesn't make sense to me why they have 1 - cosine.
Homework Statement
Using energy method,
derive the equation of motion for the pendulum which consists of the slender uniform rod of mass m and the bob of mass M. assume small oscillations, and neglect the radius of the bob.
***see attachment for diagram***
Homework Equations
[tex] I_o = \frac{1}{3}mL^2 + ML^2 [/tex] is the moment of inertia
[tex] V = mgh [/tex]
is the gravitational potential energy
[tex] T = \frac{1}{2}I_o \omega^2 = \frac{1}{2}I_o \dot{\theta}^2 [/tex]
is the kinetic energy
[tex] \frac{d}{dt}(T+V)=0 [/tex]
to get equation of motion
The Attempt at a Solution
My expression for V is this;
[tex] V = -mg\frac{L}{2}cos(\theta)-MgLcos(\theta) [/tex]
where I have taken the datum as being at the pivot acting postive up. This is different to the solution, which has written[tex] V_{solution} = mg\frac{L}{2}(1-cos(\theta))+ MgL(1-cos(\theta)) [/tex]
I don't understand why they have 1 - cos(theta). Wouldn't you just want the cosine of the angle?
Anyway, if I continue to the derivtive step (doing the small angle approximation), this doesn't seem to have an effect. So...
[tex] \frac{d}{dt}(T+V)=\frac{d}{dt}\left ( \frac{1}{2}(M+\frac{m}{3})L^2\dot{\theta}^2 -mg\frac{L}{2}cos(\theta)-MgLcos(\theta)\right ) =0 [/tex]
which yields, after a lot of manipulation,
[tex] \ddot{\theta}+\frac{3g(m+2M)}{2L(m+3M)}\theta = 0 [/tex]
which is what the textbook says is correct.
is the textbooks expression for the potential energy wrong in this case? or did I get lucky in getting the right answer? It doesn't make sense to me why they have 1 - cosine.
Attachments
Last edited: