Equilibrium: Minimum Cable Length

[ledphones]

Homework Statement

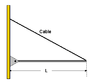
The above figure shows a uniform iron beam of mass 253 kg and length L = 3 m. The cable holding the beam in place can take a tension of 1300 N before it breaks. Use the Young's Modulus for steel to be 200e9 N/m2. (You may ignore the small mass of the cable in this calculation.) a)What minimum length of the cable?
Lengthmin= m

HELP: How will the torque placed on the beam by the cable depend on the angle between the cable and the beam??
b)Assume the cable is made of steel and has a diameter of 1". How much will it stretch before it breaks?
Δmax = cm

HELP: Young's modulus for steel is 200X109N/m2.

Homework Equations

The Attempt at a Solution

for a)

I set the forces in the x up like :
mgcos(phi)-Fcos(theta)=0

y:
Fsin(phi)+Tsin(theta)-W=0

torque
-Wdsin(180)+TLsin(theta)=0

where phi is the angle of the wall the normal force and theta is the angle of the cable and the beam. i don't know where x comes into play

for part b i think it would be like this

stress=1050/(1.27^2pi)

stress/20000000=strain

change in L will be strain*the L from part a

 

[Delphi51]

torque
-Wdsin(180)+TLsin(theta)=0

I don't follow the first term. It should be the weight times the distance from the pivot to the center of mass, which is L/2. There is no angle involved since the weight acts perpendicular to the beam. I agree with your second term. Solve for the angle theta, from which you can calculate the length of the cable.