You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Equilibrium Stat Mech Vs. Kinetics
- Thread starter bolbteppa
- Start date
-
- Tags
- Equilibrium Kinetics Stat mech
AI Thread Summary
The discussion centers on the interpretation of a passage from Landau's work regarding the behavior of subsystems within a closed macroscopic system. It emphasizes that while subsystems interact with their surroundings, the complexity of these interactions makes exact solutions impractical. Instead, the passage introduces the concept of the ergodic hypothesis, suggesting that over a long time, a subsystem will explore all possible states in its phase space. This leads to the conclusion that the probability of finding the subsystem in a specific state can be determined by the time spent in that state relative to the total observation time. The inquiry seeks clarity on how this relates to the behavior of multiple harmonic oscillators in phase space.
Physics news on Phys.org
bolbteppa
- 300
- 41
Related to this point (functioning as something which might explain the above more deeply), what is the actual meaning of this passage from Landau vol. 5:
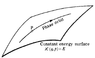
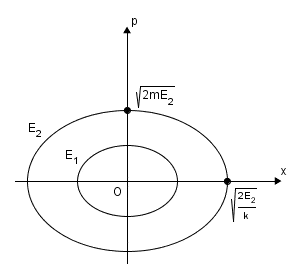
Again as an example, take H(q,p) = \tfrac{p^2}{2m}+\tfrac{k}{2}q^2 = E_0 as the Hamiltonian for a single particle, the trajectory of the particle, i.e. the set of all possible states, is an ellipse in (q,p) phase space.
Extend it to n particles and we'll have a Cartesian product of n ellipses, or a big ellipsoid, visualized as
What in the world does that passage really mean, in terms of n harmonic oscillators respresented as a single curve in phase space? I can't make actually make any sense out of it.
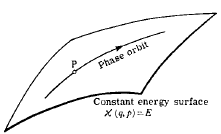
Let us now consider a macroscopic body or system of bodies, and assume that the system is closed, i.e. does not interact with any other bodies. A part of the system, which is very small compared with the whole system but still macroscopic, may be imagined to be separated from the rest; clearly, when the number of particles in the whole system is sufficiently large, the number in a small part of it may still be very large. Such relatively small but still macroscopic parts will be called subsystems. A subsystem is again a mechanical system, but not a closed one; on the contrary, it interacts in various ways with the other parts of the system. Because of the very large number of degrees of freedom of the other parts, these interactions will be very complex and intricate. Thus the state of the subsystem considered will vary with time in a very complex and intricate manner.
An exact solution for the behaviour of the subsystem can be obtained only by solving the mechanical problem for the entire closed system, i.e. by setting up and solving all the differential equations of motion with given initial conditions, which, as already mentioned, is an impracticable task. Fortunately, it is just this very complicated manner of variation of the state of subsystems which, though rendering the methods of mechanics inapplicable, allows a different approach to the solution of the problem.
A fundamental feature of this approach is the fact that, because of the extreme complexity of the external interactions with the other parts of the system, during a sufficiently long time the subsystem considered will be many times in every possible state. This may be more precisely formulated as follows. Let dp dq denote some small "volume" of the phase space of the subsystem, corresponding to coordinates q, and momenta p, lying in short intervals dq, and dp,. We can say that, in a sufficiently long time T, the extremely intricate phase trajectory passes many times through each such volume of phase space. Let dt be the part of the total time T during which the subsystem was in the given volume of phase space dp dq. When the total time T increases indefinitely, the ratio dt/T tends to some limit w = lim dt/T.
This quantity may clearly be regarded as the probability that, if the subsystem is observed at an arbitrary instant, it will be found in the given volume of phase space dpdq.
Again as an example, take H(q,p) = \tfrac{p^2}{2m}+\tfrac{k}{2}q^2 = E_0 as the Hamiltonian for a single particle, the trajectory of the particle, i.e. the set of all possible states, is an ellipse in (q,p) phase space.
Extend it to n particles and we'll have a Cartesian product of n ellipses, or a big ellipsoid, visualized as
What in the world does that passage really mean, in terms of n harmonic oscillators respresented as a single curve in phase space? I can't make actually make any sense out of it.
TSC
- 39
- 1
This is the ergodic hypothesis.
The rope is tied into the person (the load of 200 pounds) and the rope goes up from the person to a fixed pulley and back down to his hands. He hauls the rope to suspend himself in the air. What is the mechanical advantage of the system? The person will indeed only have to lift half of his body weight (roughly 100 pounds) because he now lessened the load by that same amount. This APPEARS to be a 2:1 because he can hold himself with half the force, but my question is: is that mechanical...
Some physics textbook writer told me that Newton's first law applies only on bodies that feel no interactions at all. He said that if a body is on rest or moves in constant velocity, there is no external force acting on it. But I have heard another form of the law that says the net force acting on a body must be zero. This means there is interactions involved after all. So which one is correct?
Hello!
I have a question regarding a beam on an inclined plane. I was considering a beam resting on two supports attached to an inclined plane. I was almost sure that the lower support must be more loaded. My imagination about this problem is shown in the picture below.
Here is how I wrote the condition of equilibrium forces:
$$
\begin{cases}
F_{g\parallel}=F_{t1}+F_{t2}, \\
F_{g\perp}=F_{r1}+F_{r2}
\end{cases}.
$$
On the other hand...
Similar threads
- Replies
- 8
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 10
- Views
- 3K
- Replies
- 2
- Views
- 1K
- Replies
- 2
- Views
- 1K
- Replies
- 9
- Views
- 5K
- Replies
- 1
- Views
- 367
- Replies
- 8
- Views
- 2K
- Replies
- 6
- Views
- 2K
- Replies
- 16
- Views
- 2K
Hot Threads
-
I Explain Bernoulli at the molecular level?
- Started by user079622
- Replies: 251
- Classical Physics
-
B Simple mass/scale puzzle
- Started by DaveC426913
- Replies: 206
- Classical Physics
-
I How deep does it need to go for a physics theory to be consistent?
- Started by Aleberto69
- Replies: 50
- Classical Physics
-
I Solving a momentum problem where masses change after the collision
- Started by rdemyan
- Replies: 35
- Classical Physics
-
B Torque Calculation - Not a basic application
- Started by TeeBeeCee
- Replies: 37
- Classical Physics
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math