A Equipartition theorem and Coupled harmonic oscillator system

[Karthiksrao]

TL;DR Summary

Does equipartition theorem hold true in a coupled harmonic oscillator system connected to heat bath ?

Dear all,

While simulating a coupled harmonic oscillator system, I encountered some puzzling results which I haven't been able to resolve. I was wondering if there is bug in my simulation or if I am interpreting results incorrectly.

1) In first case, take a simple harmonic oscillator system as follows: mass m, spring constant k, undamped connected to another spring mass system with same mass m, same spring constant k, undamped again; and the two systems are connected via a spring with some coupling constant.

I now excite the system by giving a small displacement $x_0$ to the first mass, and analyze the energy of the the two systems as: $\frac{1}{2} k x_1^2(t) + \frac{1}{2} m v_1^2(t)$ and $\frac{1}{2} k x_2^2(t) + \frac{1}{2} m v_2^2(t)$. The displacements and velocities calculated as per equations of motion.

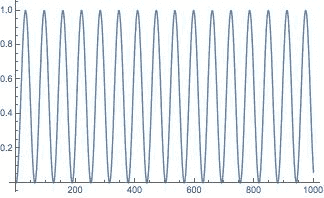
Clearly the energy of the two oscillators will oscillate over time, and this is reflected in the plot of energy of the second oscillator system $\frac{1}{2} k x_2^2(t) + \frac{1}{2} m v_2^2(t)$ attached below (Y-axis has been normalized with respect to the intial excitation energy $\frac{1}{2} k x_0^2(t)$, and x-axis is in time units

2) I now want to simulate the effect of connecting the two spring-mass systems to two heat baths which are equivalent in every way, and whose effect is to broaden the resonant frequencies of the two systems. So rather than the two systems interacting at a single resonant frequency the two systems are exchanging energy via interaction over a finite range of frequencies centered around the resonant frequency - and the energy of the two systems can be tracked by adding up contributions of all these frequencies which are interacting with one another. This dephasing results in loss in coherence in energy transfer and over time the energy in the two systems stabilizes to a certain value.

Here is the interesting part: since the two systems are symmetric/equivalent in every way - I was expecting that over time the two oscillator systems will stabilize to have equal energy between them - irrespective of the coupling strength. Note that the only asymmetry is in the initial condition (where the intial excitation energy is given to the first spring).
However, what I am noticing is different: the final energy distribution between the two oscillatory systems seems to depend on the coupling constant. A higher coupling constant will result in equal partition of energy between the two systems. But a lower coupling constant ensures that the first system will retain much of the initialization energy after a long time interval.

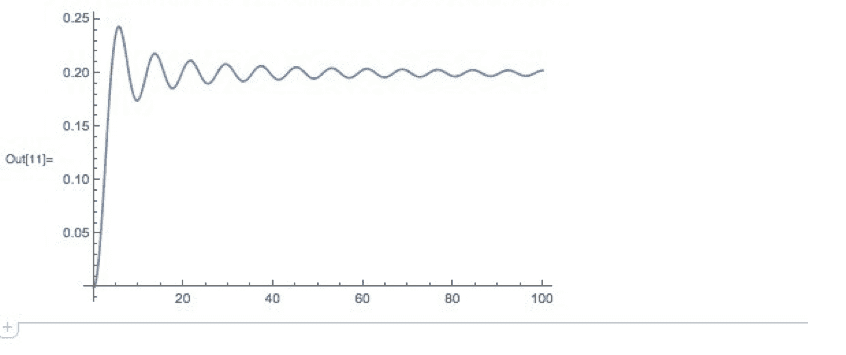
The plot below shows the energy of the second oscillator calculated as: $\frac{1}{2} k x_2^2(t) + \frac{1}{2} m v_2^2(t)$ as a function of time for the weak coupling case. For stronger coupling the equilibrium is around 0.5. I believe this discrepancy has little to do with the energy stored in the coupling spring since situation is similar even if instead of plotting the energy of the oscillators, I had plotted the energy of the individual normal modes of the system using normal coordinates.

Can somebody comment if this observation for weak coupling does not violate any law of thermodynamics ?

This seems strangely reminiscent of the Fermi-Pasta-Ulam system where, as explained here:
https://www.jstor.org/stable/27859329?seq=1#metadata_info_tab_contents
in Page 9 of the document, "
"FPU would have observed that equipartition had they used either stronger nonlinearities (yielding stronger interactions between different modes) or initial pulses with more energy.". This of course is a different system with nonlinear interactions. But I'm wondering if for linear systems as well, we need strong interactions to achieve equipartition between the modes. What do you think ?

Thanks.

 

[jrmichler]

take a simple harmonic oscillator system as follows: mass m, spring constant k, undamped connected to another spring mass system with same mass m, same spring constant k, undamped again; and the two systems are connected via a spring with some coupling constant.

Diagram, we need a diagram. And what is a "coupling constant"?

connecting the two spring-mass systems to two heat baths

We need anther diagram. Is a heat bath anything like a viscous damper?

 

[hutchphd]

Why is this a surprise?
If the coupling were zero what would you expect? Can you define a characteristic time from the "coupling constant?"

 

[Karthiksrao]

I see no option to edit the question. (Is it possible?) So I will add the information you have requested here:

@jrmichler

$\xi$ is a parameter which will decide the coupling strength of the intermediate spring. $\xi \ll 1$ suggests weak coupling

By heat bath - I mean the effect of environment on the two oscillator systems. Not sure how I can adequately represent in a diagram.

Regarding, the effect of heat bath, I am looking at the energy transfer dynamics between the two harmonic oscillator systems during a time scale less than the time scale over which the bath absorbs energy. As such we can assume that the bath does not provide any viscous damping. The only effect of the environment/bath is to broaden the resonance frequency. So that now, the two oscillators are exchanging energy over a spectrum of frequencies which results in dephasing.

Of course, if I want to include the viscous damping effect of the environment, I can always include a $-m \gamma \dot{x_1}$ and $-m \gamma \dot{x_2}$ terms in the equations of motion for the two masses. However, after a period of time, the bath will absorb all the excitation energy and the energy of the oscillator will just go to zero. I am not interested in this part. I am more interested in the energy dynamics between the oscillators. As such I have taken $\gamma =0$

@hutchphd
If coupling is zero, then there will be no exchange of energy of the two systems. As such oscillator system 1 will retain the initial excitation energy and oscillator system 2 will be stationary.

But even if we provide a small coupling term, then the systems will exchange energy. What I was expecting was: the two systems attain equipartition over a long time interval when coupling is small. For higher coupling strength : the two will attain equipartition over a shorter time interval.

But this is not what is observed. That brings the question: what are the necessary conditions for equipartition to hold true ? What would you change in this system for you to see equipartition ?

Thanks.