Error Analysis of Modern Gram Schmidt Technique -code bug

[SchrodingersMu]

Hi all,

I am to compute A = QR using the Modified Gram-Schmidt algorithm. I need to find the error using

the one norm of : (Q transpose * Q) - I.

Here is my code:

%Modern Gram Schmidt
p=zeros(5,5);
e=zeros(5,5);
g=zeros(5,5);

for k=1:n;
    p(:,k)=(A(:,k));
end
%j=k, i=u, r=g, q=e, v=p
for u=1:n
    g(u,u)=norm(p(:,u),2);
    e(:,u)=p(:,u)/g(u,u);
    for k=u+1:n
        g(u,k)=e(:,u)'*p(:,k);
        p(:,k)=p(:,k)-(e(:,u)*g(u,k));
    end
end

W=((p*p')-I);
errormod=norm(W,1);

save errorMGS.dat errormod -ascii

I am getting an errormod of 1.00 . It obviously should be way less than this. I can't see what I am doing wrong, though. I modeled my code after an example proided by my prof: (The left part of the powerpoint)

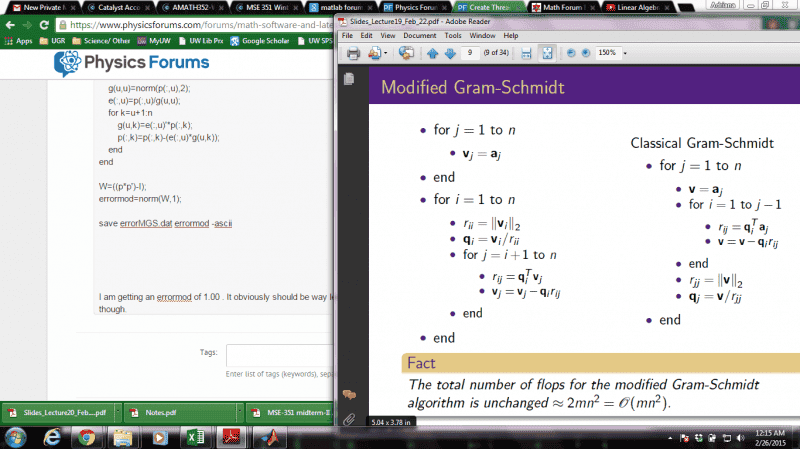
Any help is appreciated!

 

[RUber]

Reading through your code, it looks like you are saving the p as the full-scale matrix, where e is the normalized matrix.
Try setting p(:,u)=e(:.u) at the end of the loop for each u.