Evaluate 2 logistic functions for the best x to minimize OR.

[Adel Makram]

Here are conditions I use to define my problem:
1) I use cumulative distribution of 2 logistic functions g₁(x) and g₂(x) with g₂ is translated to the right of the g₁(x) on x-axis.
2) I make a transformation to eliminate both tails of the function which will not have a significant contribution to the result, so my transformation is:

f(x) = g(x) - g(α) / g(1-α) - g(α).
where g(α) can be chosen to be equal to 0.05 and g(1-α)= 0.95.

3) g₂(x) is translated with amount r to the right side of g₁(x).

The aim of the study is to determine the best odd ratio (OR) between g₁(x)/1-g₁(x) and g₂(x)/1-g₂(x). In other words, I am looking for minimizing this ratio by taking the first derivatives and making it equal to zero and then calculate x.
to make the matter more simpler, I assumed that the scale parameters of both g₁(x) and g₂(x) are equal to each other.

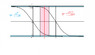
surprisingly, after calculation I got x=-∝ which minimizing the ratio against the intuition that x should equal to 1/2 r. Please look at the attached diagram where the area with pink shade represents the interval where x should lie. On both boundaries of this area, OR will be ∝ and OR should come to a minimum at the required x. I made an initial transformation y=e^-x and n=y^k where k is the scale parameter which I put it to be the same in 2 functions. So I got n=0 (trivial solution) which means y=0 only at x=-∝. So, how come the calculation came opposite to the right intuition that x should = 1/2 r.[/SUB][/SUB][/SUB][/SUB][/SUB][/SUB][/SUB][/SUB]

 

[mfb]

The functions get very close to 0 and 1 exponentially, I'm not surprised to see their ratio be optimized "at infinity".

 

[Adel Makram]

The functions get very close to 0 and 1 exponentially, I'm not surprised to see their ratio be optimized "at infinity".

This is correct for the original function g(x) but not for the transformed function f(x). Because f(x) is exactly equal to 0 at x= α and f(x) is exactly equal to 1 at x=-α,,, {sorry for the typing mistake in the original post, the transformation should be f(x) = g(x) - g(α) / g(-α) - g(α)}. where α corresponds to the value of x where the function has the value of 0.05 and -α corresponds to te value of x where the function has 0.95
Now at the interval x∈{r-α , α} the odd ratio defined as f₂(x)/1-f₂(x) / f₁(x)/1-f₁(x) approach infinity at both boundaries, namely, at x= α and x= r-α. But converge to a minimum at x=x_c which I call it critical x. And my project is to find x_c which I found it equals to -∝ which means there is something wrong in my calculation.

 

[mfb]

Then your ratio gets even more extreme until it gets undefined - and you'll have to consider at least 5 different ranges individually. Did you do that?

It would help to see what you did in more detail. And what exactly do you want to find, and why?

 

[Adel Makram]

Then your ratio gets even more extreme until it gets undefined - and you'll have to consider at least 5 different ranges individually. Did you do that?

It would help to see what you did in more detail. And what exactly do you want to find, and why?

Thank you for your help, hereby I attach a word document explaining my calculation with 2 graphs.

 

[mfb]

All those substitutions make the analysis messy, especially as I don't see a system in them.

How can v=e^k2 appear as factor anywhere? k2 is always together with either x or r.

For symmetry, I think it would be easier to shift one equation by -r/2 and one by r/2.

 

[Adel Makram]

for f₂(x), there is an exponential term e^-k2(x-r) which=e^{-k2 x} e ^{k2 r} = y^k2 v = nv
(it was a typing mistake that I wrote v=e^k2 it is suppose to be e ^{k2 r} ).

 

[mfb]

Ah just a typo, okay.

I still think using the symmetry would make the analysis easier.

 

[Adel Makram]

Ah just a typo, okay.

I still think using the symmetry would make the analysis easier.

I followed your advice and I found that I was wrong in my calculation. Yes true I found that the final calculation of n reduced to n=√C/A which is equal to 1. This means that e^-kx=1 which will be satisfied at x=0 as intuitively though.

Next step which is very important, is to calculate the critical x when k1≠k2. This would be more challenging.

 

[Adel Makram]

I went through a long calculation this time when k1≠k2. The final equation is in the form of polynomial of e^-x.
It comes in this form; k₁ A e^-(2k2+k1)x + k2 B e^-(2k1+k2)x + C (k1-k2) e^-(k2+k1)2x + D K1 e^-(k1)x + E k2 e^-(k2)x=0

where A, B, C, D and E are coefficients of α, e^{1/2 K₂ r} and e^{-1/2 K₁ r}. K1 and k2 are (inverse of scale parameters of 2 logistic functions, f1(x) and f2(x), respectively, r is the distance between the 2 functions means.

So any general solution of this polynomial in x?

 

[mfb]

The k-prefactors can get included into the A to E parameters.

Using $y=e^{-k_1 x}$ and $f=\frac{k2}{k1}$, we get the following terms (all with prefactors):
y*y^(2f)
y^2*y^f
y^2*y^(2f)
y
y^f
Unless the prefactors match very nicely in some special way, I would be surprised by a general solution. Note that f=2 gives you powers 1, 2, 4, 5, 6, after dividing by y this is nearly a general polynomial of 5th order where no general closed solutions exist.

 

[Adel Makram]

But this is not going to match the OR (odd ratio) curve which it should have a minimum in the range {r-α, α}.
I expect the first derivatives of OR to have only one root at critical x, x_c not five roots.
My formula for minimizing OR is ∂OR/∂x = (∂OR/∂n)(∂n/∂x) + (∂OR/∂m)(∂m/∂x)
where, n= e^-k2x, m= e^-k1x
∂n/∂x= -k2 n, ∂m/∂x= -k1 m.
This would reduce the equation I got in the post#10 into; A mn² + B(1-k2/k1)mn + Cm + D(k2/k1) m²n + fF n=0

 

[mfb]

Some of the roout would be an artifact of the calculation process and/or complex.

It could be interesting to calculate some numerical examples, there might be some easy function showing up, at least as approximation.