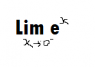Evaluate lim e^x when x approaches zero from negative

[Outrageous]

Homework Statement

What is the limit of e^x when x approaches zero from negative side

Homework Equations

The Attempt at a Solution

Taylor series? Then the answer is put all x= 0 , and the answer is 1, but why the question ask from negative side??

Thank you very much

 

[mfb]

Can you use that e^x is continuous? This would allow to use e^0.
If not, what do you know about the exponential function?

That is a strange question.

 

[Outrageous]

The question didn't say, but if it is continuous then I can use Taylor series for e^x . Then just substitute all x with zero? And get answer 1 . Then what is the point to have x approaches zero? Or should I use graph ?
Thank you

 

[Ray Vickson]

The question didn't say, but if it is continuous then I can use Taylor series for e^x . Then just substitute all x with zero? And get answer 1 . Then what is the point to have x approaches zero? Or should I use graph ?
Thank you

What are the *definitions* of e and e^x that you are allowed to use? What facts about e^x are you allowed to use? The point is: how you deal with the problem depends crucially on what properties of e^x you know already. The question you present is almost meaningless, because you leave out so much important information.

 

[HallsofIvy]

The question didn't say, but if it is continuous then I can use Taylor series for e^x .

It is not sufficient for a function to be continuous in order that it HAVE a Taylor series. But the Taylor series has nothing to do with the question.

Then just substitute all x with zero? And get answer 1 . Then what is the point to have x approaches zero? Or should I use graph ?
Thank you

Do you understand what "continuous" means? The definition of "continuous" is that that the limit, as x goes to a, is equal to the value of the function, f(a). That is the point of "x approaches 0"- you evaluate the function at x= 0. If you meant to ask "why approach 0 from the negative side" there doesn't appear to be any special reason except perhaps to see if you really understood the idea of "limit". If f(x) is continuous at x= a (and e^x is continuous for all x), then, by definition, \lim_{x\to a} f(x)= f(a), and, if the limit exists, \lim_{x\to a^-}f(x)= \lim_{x\to a^+} f(x)= \lim_{x\to a} f(x).

 

[mtayab1994]

Well e^x is differentiable therefore continuous at 0. So the limit at left of 0 is the same as the right of 0.

 

[Outrageous]

Thank you guys.

This is the whole question that I get from past year exam .
Evaluate lim e^x when x approaches zero from negative.

Do you understand what "continuous" means? The definition of "continuous" is that that the limit, as x goes to a, is equal to the value of the function, f(a). That is the point of "x approaches 0"- you evaluate the function at x= 0. If you meant to ask "why approach 0 from the negative side" there doesn't appear to be any special reason except perhaps to see if you really understood the idea of "limit". If f(x) is continuous at x= a (and e^x is continuous for all x), then, by definition, \lim_{x\to a} f(x)= f(a), and, if the limit exists, \lim_{x\to a^-}f(x)= \lim_{x\to a^+} f(x)= \lim_{x\to a} f(x).

Thank you . I am too eager to solve problem until forget all the important basic knowledge.