- #1
Maggie_s2020
- 2
- 0
Hello, I have been trying to solve the top line equation to get the result (the bottom line). I am searching for a clue (the steps) on how to obtain those four brackets as a result.
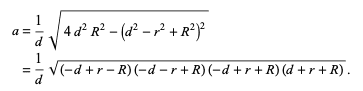
Last edited by a moderator:
THANK YOU SO SO SO MUCH! BLESS YOU!skeeter said:factoring the expression within the radical just involves the difference of squares ...
$4d^2R^2 - (d^2-r^2+R^2)$
$(2dR)^2 - (d^2-r^2+R^2)^2$
$[2dR -(d^2-r^2+R^2)] \cdot [2dR + (d^2-r^2+R^2)]$
$[-(d^2-2dR+R^2) + r^2] \cdot [(d^2+2dR+R^2) - r^2]$
$[r^2-(d-R)^2] \cdot [(d+R)^2 - r^2]$
$[(r-d+R)(r+d-R)] \cdot [(d+R-r)(d+R+r)]$
multiply the two middle factors by (-1) ...
$(-d+r+R)(-d-r+R)(-d+r-R)(d+r+R)$
The purpose of expanding and simplifying brackets is to simplify algebraic expressions and make them easier to work with. This process involves distributing the terms inside the brackets to the terms outside the brackets and then combining like terms to simplify the expression.
The steps for expanding and simplifying brackets are as follows:
1. Multiply the term outside the brackets by each term inside the brackets.
2. Use the distributive property to distribute the terms inside the brackets.
3. Combine like terms to simplify the expression.
You should expand and simplify brackets when working with algebraic expressions that contain terms inside brackets. This process is necessary to fully simplify the expression and solve for the variable.
No, brackets must be expanded before they can be simplified. This is because the distributive property, which is used to expand the brackets, must be applied first in order to distribute the terms inside the brackets. Once the brackets have been expanded, the terms can then be combined and simplified.
Some common mistakes to avoid when expanding and simplifying brackets include:
- Forgetting to distribute the terms inside the brackets to the terms outside the brackets.
- Combining unlike terms.
- Forgetting to include negative signs when distributing negative terms inside the brackets.
- Not simplifying the expression fully by combining like terms.
It is important to carefully follow the steps and pay attention to signs when expanding and simplifying brackets to avoid these mistakes.