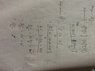Explain how do we get standard error.

[Outrageous]

Homework Statement

I know that standard error is to calculate how the sample deviate from the population.
But standard deviation divide √n ,then will get it.
And I don't understand why there is a T/n from the picture I uploaded. Please help

Homework Equations

Standard error x sqrt(n) = Standard deviation

The Attempt at a Solution

 

[haruspex]

I'm not sure whether you understand that the "variance of T" is not the variance of a single sample of n; it's the variance of a random variable T each value of which is defined to be the sum of n independent trials of X.
I'm also unsure what you mean by standard error here. Standard error is usually used in reference to some statistic, such as an estimate of the mean. Your attachment doesn't mention standard error.
I assume that T/n is of interest because it could be used for estimates of the mean of X. The standard deviation of the r.v. T/n would then be the standard error of the mean so estimated.

 

[Outrageous]

Not really understand.
Can you please teach me this first:
A sample of 5 students from 50 students.
The score of 5 students for math are recorded.
Mean of 5 students is 62.
sample σ from 5 students =27.44
The standard deviation of 50 students is 17.
Standard error = 17/√5.

What is the standard error here used for ?
This represents how well this sample deviate from the population?

So if I can get the mean of 50 students ,x
Then x-62 will be standard error?
Please guide . Thank you

 

[haruspex]

Not really understand.
Can you please teach me this first:
A sample of 5 students from 50 students.
The score of 5 students for math are recorded.
Mean of 5 students is 62.
sample σ from 5 students =27.44
The standard deviation of 50 students is 17.
Standard error = 17/√5.

What is the standard error here used for ?
This represents how well this sample deviate from the population?

If I'm reading that correctly, you happen to know (by some means) that the s.d. of the whole population is 17. If you attempt to estimate the mean of the whole population by taking a sample of 5, the standard error in the resulting number is 17/√5. That is, if you were to take lots of samples of 5 and look at the calculated means, their standard deviation would be about 17/√5.
But notice I have not made use of the 27.44. In practice, if you don't know the mean of the whole population then it's very unlikely that you know its s.d. So you'll be estimating both the mean and the s.d. from the sample.

So if I can get the mean of 50 students ,x Then x-62 will be standard error?

No, standard error is the square root of the expected variance of the calculated statistic. Since the underlying population has a variance of 17², the sum of 5 samples has an expected variance of 5*17², and the average of 5 samples has an expected variance of (5*17²)/5² = 17²/5. The square root of that is 17/√5.

 

[Outrageous]

If you attempt to estimate the mean of the whole population by taking a sample of 5, the standard error in the resulting number is 17/√5. That is, if you were to take lots of samples of 5 and look at the calculated means, their standard deviation would be about 17/√5.

Thank you.

the sum of 5 samples has an expected variance of 5*17², and the average of 5 samples has an expected variance of (5*17²)/5² = 17²/5.

This is totally same as what I uploaded, I don't understand why the average of 5 samples has an expected variance of (5*17²)/5² = 17²/5 ?

 

[haruspex]

Average of N samples is ƩX_i/N. Expected variance of this is E[(ƩX_i/N)²] - (E[ƩX_i/N])² = (E[(ƩX_i)²] - (E[ƩX_i])²)/N².
Leaving off the factor 1/N² for now:
E[(ƩX_i)²] - (E[ƩX_i])² = E[ƩX_i²+Ʃ_i≠jX_iX_j]-(ƩE[X_i])² = E[ƩX_i²]+E[Ʃ_i≠jX_iX_j]-(Nμ)² = ƩE[X_i²]+Ʃ_i≠jE[X_iX_j]-(Nμ)²
= N(σ²+μ²)+N(N-1)μ²-(Nμ)² = Nσ²
So expected variance of average is σ²/N

 

[Outrageous]

Average of N samples is ƩX_i/N. Expected variance of this is E[(ƩX_i/N)²] - (E[ƩX_i/N])² = (E[(ƩX_i)²] - (E[ƩX_i])²)/N².

Is that the definition? I mean we must define the variance in this way?

 

[haruspex]

Is that the definition? I mean we must define the variance in this way?

The variance of a set of numbers is the mean square difference from the mean: Ʃ(x_i-μ)²/N, where μ = Ʃx_i/N. It's not hard to show that this is the same as (Ʃx_i²/N) - μ². Or, writing in terms of expectations of a r.v., E[X²]-(E[X])².

 

[Outrageous]

I am not sure the expected is the mean or?
Can you please guide more .
Really thank