- #1
gony rosenman
- 11
- 4
Explaining a signal converting circuit
- Thread starter gony rosenman
- Start date
Click For Summary
Discussion Overview
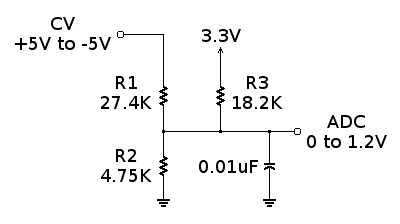
The discussion revolves around a circuit designed to convert a signal from a range of [-5, 5] V to [0, 1.2] V. Participants explore the workings of this circuit, seeking to understand its operation from both a theoretical and practical perspective.
Discussion Character
- Technical explanation
- Conceptual clarification
Main Points Raised
- One participant describes the circuit as a "resistive summer" or "passive averager" and provides a link to a resource for further reading.
- Another participant confirms the circuit's classification as a resistive summer and presents a nodal analysis equation to illustrate its function, stating that the output can be expressed as ADC = 0.12*CV + 0.6.
- This participant elaborates on the operation of the circuit, explaining the need for level shifting and attenuation, and invokes the principle of superposition to analyze the circuit's behavior under different conditions.
- A later reply expresses gratitude for the clarity of the explanation provided, indicating that the information was well-received.
Areas of Agreement / Disagreement
Participants generally agree on the classification of the circuit and the explanation of its function, but there is no explicit consensus on all aspects of the operation or the underlying principles discussed.
Contextual Notes
The discussion includes assumptions about the linearity of the system and the application of the principle of superposition, which may not be universally applicable without further context.
- #2
lewando
Homework Helper
Gold Member
- 1,366
- 145
It is a "resistive summer" or "passive averager" described in this https://www.allaboutcircuits.com/textbook/semiconductors/chpt-8/averager-summer-circuits/.
- #3
analogdesign
Science Advisor
- 1,150
- 370
It is indeed a resistive summer. To see that it works (not HOW it works), you can write a nodal analysis equation (using Kirchhoff's current law) at node "ADC" and you will find it gives the function:
ADC = 0.12*CV + 0.6, as desired.
But you want to know HOW it works, here is a more intuitive explanation that is more in the spirit of how an analog engineer would approach the problem (rather than showing you a plug-and-chug simplification of a node equation).
First you need to appreciate that to do the level shifting you really want to do two different things. First, you want to set the "analog ground", or average value, to 0.6 (because that is midway between 0 and 1.2V). Second, you want to attenuate the magnitude of the CV range from 10 V (that is, 5V - (-5V) )to 1.2V. In other words, you want to multiply CV by a gain of 1.2 / 10 = 0.12 and shift its DC level from 0 to 0.6.
OK. Now, to see how the circuit works to do these things we invoke the principle of superposition. This principle states that if we have a linear system then we can calculate the response to each source independently, setting the other sources to zero (in this case CV and the 3.3 V supply) and then add them to get the composite response.
So, we get the baseline by looking at the 3.3 V supply. From the point of view of the 3.3 V supply, we see the 27.4 k and 4.75 k resistors are in parallel (remember we set CV = 0 here). Then, we have a voltage divider and ADC = ((4.75 || 27.4) / ( (4.75 || 27.4) + 18.2)) * 3.3. Now, 4.75 || 27.4 = 4.05 so we have ADC = (4.05 / ( 4.05 + 18.2))* 3.3 = 0.18 *3.3 = 0.6, as desired.
We get the attenuation by looking at what CV "sees". In this case, the 4.75k resistor is in parallel with the 18.2k resistor (remember we set the 3.3 volt source to 0 here). Then we proceed as above, ADC =((4.75 || 18.2) / ( (4.75 || 1.8) + 27.4)) * CV. Or, calculating it out, ADC = 0.12 * CV.
Adding the two responses together (invoking the principle of superposition) we have:
ADC = 0.12*CV + 0.6, which is exactly what we wanted in the first place.
Make sense?
ADC = 0.12*CV + 0.6, as desired.
But you want to know HOW it works, here is a more intuitive explanation that is more in the spirit of how an analog engineer would approach the problem (rather than showing you a plug-and-chug simplification of a node equation).
First you need to appreciate that to do the level shifting you really want to do two different things. First, you want to set the "analog ground", or average value, to 0.6 (because that is midway between 0 and 1.2V). Second, you want to attenuate the magnitude of the CV range from 10 V (that is, 5V - (-5V) )to 1.2V. In other words, you want to multiply CV by a gain of 1.2 / 10 = 0.12 and shift its DC level from 0 to 0.6.
OK. Now, to see how the circuit works to do these things we invoke the principle of superposition. This principle states that if we have a linear system then we can calculate the response to each source independently, setting the other sources to zero (in this case CV and the 3.3 V supply) and then add them to get the composite response.
So, we get the baseline by looking at the 3.3 V supply. From the point of view of the 3.3 V supply, we see the 27.4 k and 4.75 k resistors are in parallel (remember we set CV = 0 here). Then, we have a voltage divider and ADC = ((4.75 || 27.4) / ( (4.75 || 27.4) + 18.2)) * 3.3. Now, 4.75 || 27.4 = 4.05 so we have ADC = (4.05 / ( 4.05 + 18.2))* 3.3 = 0.18 *3.3 = 0.6, as desired.
We get the attenuation by looking at what CV "sees". In this case, the 4.75k resistor is in parallel with the 18.2k resistor (remember we set the 3.3 volt source to 0 here). Then we proceed as above, ADC =((4.75 || 18.2) / ( (4.75 || 1.8) + 27.4)) * CV. Or, calculating it out, ADC = 0.12 * CV.
Adding the two responses together (invoking the principle of superposition) we have:
ADC = 0.12*CV + 0.6, which is exactly what we wanted in the first place.
Make sense?
- #4
gony rosenman
- 11
- 4
you , my dear sir , are an angel !
thank you for the clear and thorough explanation .
much appreciated
thank you for the clear and thorough explanation .
much appreciated