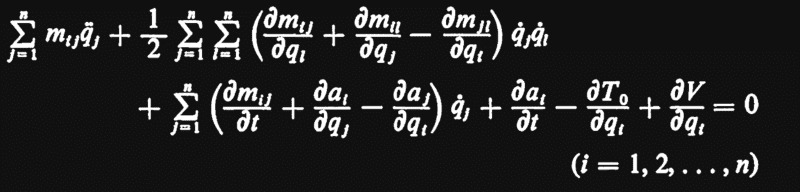SUMMARY
The discussion focuses on the explicit non-holonomic equations of motion, emphasizing the necessity of Lagrange multipliers for correctly addressing non-holonomic constraints. Participants reference Greenwood's classical dynamics and Landau and Lifshitz's volume 1 as key texts for understanding these concepts. The conversation highlights that non-holonomic constraints are local and cannot be resolved merely by selecting independent coordinates, unlike holonomic constraints. The participants express a need for a general explicit formulation of the equations of motion that incorporates these constraints.
PREREQUISITES
- Understanding of Lagrangian mechanics
- Familiarity with non-holonomic constraints
- Knowledge of Lagrange multipliers
- Basic principles of classical dynamics
NEXT STEPS
- Research the explicit forms of non-holonomic equations of motion
- Study Lagrange multipliers in the context of non-holonomic systems
- Examine case studies in Greenwood's classical dynamics
- Explore advanced topics in Landau and Lifshitz's treatment of constraints
USEFUL FOR
Students and professionals in physics, particularly those specializing in classical mechanics, as well as researchers looking to deepen their understanding of non-holonomic systems and their equations of motion.