What Does ##n(A)## Represent in Set Theory?

  • Thread starter Thread starter adjacent
  • Start date Start date
AI Thread Summary
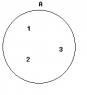
In set theory, ##n(A)## represents the number of elements in set A, regardless of their names. The discussion clarifies that the identity of the elements does not affect the count; for example, sets {1, 2, 3} and {a, b, c} both contain three elements. The confusion regarding whether to count elements as distinct based on their names is addressed, confirming that names are irrelevant for determining the count. Ultimately, the number of elements in a set is what matters, not their labels. This understanding resolves the initial doubts about the value of ##n(A)##.
adjacent
Gold Member
Messages
1,552
Reaction score
62

Homework Statement


attachment.php?attachmentid=70965&stc=1&d=1404035528.png

##n(A)##
I have some doubts.
Obviously, ##n(A)## means the number of elements in set A.
Should it be 3 or 6?

Should I consider each number to be a different element?
 

Attachments

  • set.png
    set.png
    461 bytes · Views: 448
Physics news on Phys.org
The names of the elements are irrelevant. If you change the names ##\{1,2,3\}## by ##\{a,b,c\}##, then it will have the same number of elements. Does that answer your question?
 
  • Like
Likes 1 person
micromass said:
The names of the elements are irrelevant. If you change the names ##\{1,2,3\}## by ##\{a,b,c\}##, then it will have the same number of elements. Does that answer your question?
Yes, thank you :smile:
 

Thread 'Finding the number of ways to arrange identical balls in a circle (3 different colors)'

I tried to combine those 2 formulas but it didn't work. I tried using another case where there are 2 red balls and 2 blue balls only so when combining the formula I got ##\frac{(4-1)!}{2!2!}=\frac{3}{2}## which does not make sense. Is there any formula to calculate cyclic permutation of identical objects or I have to do it by listing all the possibilities? Thanks
View full post »

Thread 'Making the denominator of a certain fraction real'

Essentially I just have this problem that I'm stuck on, on a sheet about complex numbers: Show that, for ##|r|<1,## $$1+r\cos(x)+r^2\cos(2x)+r^3\cos(3x)...=\frac{1-r\cos(x)}{1-2r\cos(x)+r^2}$$ My first thought was to express it as a geometric series, where the real part of the sum of the series would be the series you see above: $$1+re^{ix}+r^2e^{2ix}+r^3e^{3ix}...$$ The sum of this series is just: $$\frac{(re^{ix})^n-1}{re^{ix} - 1}$$ I'm having some trouble trying to figure out what to...
View full post »

Similar threads

Application of N choose K, unsure of what is happening
Replies
6
Views
2K
Determine which set is a function
Replies
3
Views
2K
Determine (with proof) the set of all prime numbers
Replies
3
Views
2K
What are the elements of set X?
Replies
2
Views
2K
Is my Proof Valid for Bijection of Finite Sets?
Replies
15
Views
3K
What Are the Combinatorial Possibilities of Glucose Polymers with n Monomers?
Replies
6
Views
1K
Proving that an Integer lies between x and y using Set Theory
Replies
15
Views
1K
Number of functions from a to b where {123} is in the range of (f)
Replies
1
Views
2K
Decompose 4x4 determinant into 24 determinants -- How many are zero?
Replies
1
Views
1K
Are the following statements true? (1) a∈{{a},{a,b}} and (2) b∈{{a},{a,b}} true?
Replies
8
Views
2K

Hot Threads

Recent Insights

Back
Top