Exponentially damped dipole - line broadening

[unscientific]

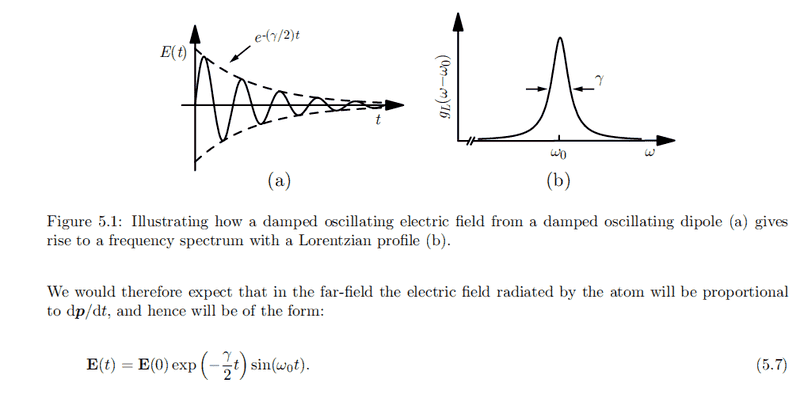
For an EM wave close to the transition frequency $\omega_{21}$, we assume the dipole moment to be exponentially damped and oscillating:

p(t) = p(0) e^{-\frac{\gamma}{2}t} cos(\omega_0 t)

Why do we expect the electric field to be proportional to $\dot p$?

Taken from my lecturer notes on laser and atomic physics:

 

[abbas_majidi]

If a dipole moment changes(it is created by charge accelerations), it emit EM wave in classic treatment. Therefore we can get E(t) proportional to dp/dt.

 

[unscientific]

If a dipole moment changes(it is created by charge accelerations), it emit EM wave in classic treatment. Therefore we can get E(t) proportional to dp/dt.

Please explain the "classical treatment".

 

[abbas_majidi]

Please explain the "classical treatment".

In classical physics accelerated charges can emit EM waves, it is used in making antenna. A dipole changes with time is a antenna and its behavior is explained by classical physics compleatly. Therefore if you use ' electric field to be proportional to $\dot p$', you consider atoms like antenna or in other words you use classical treatment of atoms.