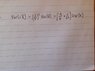CAH
- 48
- 0
Member warned multiple times about not using the homework template
See the photo of the question+ mark scheme!
I don't understand a question on finding an expression for the variance of something...
Attempt at solution: also I worked out c as (3/2) previously, which is correct
Var(U) = (3/2)^2 x Var(Xbar) = 9/4n^2 x a^2/18
I'll attach a photo of this too if it's easier to read, my problem is that I thought var(Xbar) = var(x/n) = 1/n^2 x var(x)
... But they have done var(Xbar) = 1/n x var(x) ...?
I don't understand a question on finding an expression for the variance of something...
Attempt at solution: also I worked out c as (3/2) previously, which is correct
Var(U) = (3/2)^2 x Var(Xbar) = 9/4n^2 x a^2/18
I'll attach a photo of this too if it's easier to read, my problem is that I thought var(Xbar) = var(x/n) = 1/n^2 x var(x)
... But they have done var(Xbar) = 1/n x var(x) ...?