SUMMARY
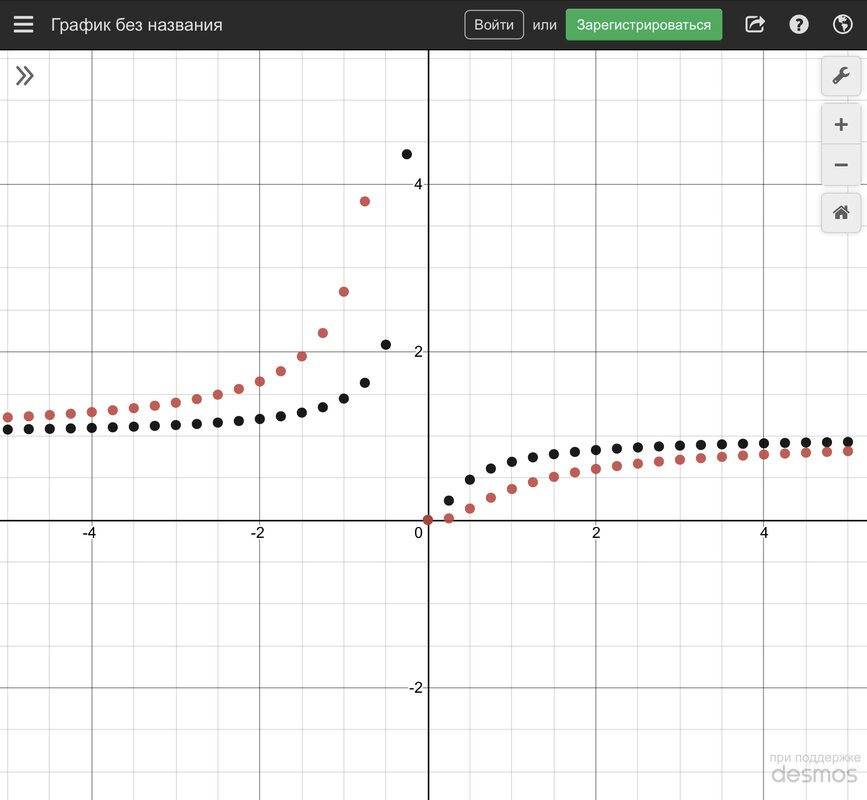
The discussion focuses on the extremums of the function defined as x raised to the power of x raised to the power of a (x^x^a). The coordinates of these extremums are plotted, with red dots representing the x-coordinates (a values) and black dots representing the y-coordinates (extremum values). Notably, the red dot at a = -0.5 has a y-coordinate of 7.389, while the red dot at a = -0.25 has a y-coordinate of 54.598. The inquiry centers on whether there exists a function that encompasses all the plotted black or red dots, with a reference to the concept of power towers for further exploration.
PREREQUISITES
- Understanding of exponential functions and their properties
- Familiarity with plotting functions and interpreting coordinate systems
- Knowledge of calculus, specifically concerning extremums and derivatives
- Basic comprehension of power towers and their mathematical implications
NEXT STEPS
- Research the properties of power towers and their convergence behavior
- Explore the concept of extremums in multivariable calculus
- Learn about advanced plotting techniques using tools like Desmos or GeoGebra
- Investigate the implications of the function x^x^a in different mathematical contexts
USEFUL FOR
Mathematicians, calculus students, and anyone interested in the behavior of complex exponential functions and their extremums.