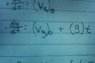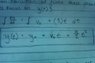Falling object far from Earths Center of Mass Problem

[bleist88]

I have been thinking about how to come up with a function of time for the n-body problem. Later I found that there still is no function of time known for the n-body problem, but I am still not sure where the brick wall for everyone is because I am quite sure my understanding has hit from very early on. I pretty much started from the ground up, where gravity is constant, and barely got through the basics. There are no explanations for what I am looking for to be found in any of my physics books, calculus book, or on the internet. I feel it is very basic yet I can't quite mathematically get anywhere, even though all of the concepts I understand clearly.

So from the start to where I am stuck:

-For a constant acceleration of gravity, such as near the Earth's surface where the acceleration of gravity = "g" [OPEN attachment A]
-Then integrate it to make the height as a function of time. [OPEN attachment B]

It is Easy so far, but when you make the height considerably far from Earth and consider it over a long fall toward earth, the Gravitational Force on the object is constantly changing and the function of time would have to respond to a function of constantly changing acceleration:
where: F = ma = GmM(1/r[1/r^2])

divide by m : a = F/m = (GM)/r^2 !

Now if we sum up the entire acceleration experienced for the object from the "initial r" to the "final r", we would simply integrate that function to get: [OPEN attachment C]

So the final velocity at any "final r" is:
V("final r") = initial V + GM[(1/ "final r") - (1/ "initial r")


This is as far as my understanding goes and now I would like to understand how to make this a function of time. Surely NASA can do something like this. They obviously know where all of the planets will be around the sun at any point in time and they obviously must have an understanding on how to send probes all over the solar system, orbiting various planets at various times and sling-shotting around this and that. Yet I can not find any literature on any of this.

ANY HELP WOULD BE GREAT. Once I got started on this not knowing how to do it has been driving me insane!

 

[Bill_K]

Now if we sum up the entire acceleration experienced for the object from the "initial r" to the "final r", we would simply integrate that function to get:
V("final r") = initial V + GM[(1/ "final r") - (1/ "initial r")

No, because the velocity would be the integral with respect to time, and you integrated the right hand side with respect to r.

What you want to do is look at the conservation of energy:

½mv² + GMm/r = the same for initial and final states

 

[rcgldr]

To give you an idea of how complext this is, the math for 2 point objects starting at rest is shown in post #8 with minor correction (3 intermediate steps) in post #15 of this thread:

https://www.physicsforums.com/showthread.php?t=360987

The math for fixed size objects by arildno in post 2 and 4 in this thread but the latex is messed up in post #2 (cleaned up in a later thread see below):

https://www.physicsforums.com/showthread.php?t=306442

arildno's math with the latex cleaned up is in post #3 of this thread:

https://www.physicsforums.com/showthread.php?t=529839

The issue for a n body system is probably related to stating the paths (position versus time) of the objects in the form of an equation. This wouldn't prevent using numerical methods based on differential equations to solve the problem.

 

[josftx]

You want to describe for example when a asteroid its falling to the Earth but from the outer space?. In this case, the gravity its not g, like you say, but its function of the distance from the objetc to the center of the earth.
$F_{gravity}=\dfrac{GM_{1}m_{2}}{(R+y(t))^{2}}$

with R the radius of the earth, M the mass of the Earth and G the universal constant and m the mass of the objetct

if you want to deduce the differential equation we must put the 2nd law of Newton

$\sum F=m_{2}\ddot{y}=\dfrac{GM_{1}m_{2}}{(R+y(t))^{2}}$
$\ddot{y(t)}-\dfrac{GM_{1}}{(R+y(t))^{2}}=0$

and if you want to put drag forces or rotational forces, put it and describe them. finally you must solve de second order ode