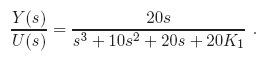The characteristic equation for your system is given by:
$$
1 + \frac{20}{s(s + 10)}\left(1 + \frac{K_1}{s}\right) = 0 \Leftrightarrow 1 + \frac
{20s + 20K_1}{s^3 + 10s^2} = 0 \Leftrightarrow 1 + L_1(s;K_1) = 0
$$
The problem here is that root-locus analysis/design is usually developed assuming a characteristic equation of the form ##1 + KF(s) = 0##, where ##K## is the parameter you want to plot the root locus for as it varies.
With that in mind:
$$
1 + \frac{20s + 20K_1}{s^3 + 10s^2} = 0 \Leftrightarrow (s^3 + 10s^2 + 20s) + 20K_1 = 0\\
\Leftrightarrow 1 + K_1\frac{20}{s^3 + 10s^2 + 20s} = 0 \Leftrightarrow 1 + K_1 L_2(s) = 0
$$
##L_1## and ##L_2## are completely different systems, but what matters is that they have the same closed-loop poles for some value of ##K_1##, i.e. their root loci are identical. You just have to be careful about what you use ##L_2## for, e.g. don't confuse it for ##L_1## when you have to simulate a reponse to some input etc.
In short: You've used the correct function for plotting the root locus for the system.
Here are some of my thoughts, in no particular order:
What is your definition of settling time? One definition defines the width of the "settling-band" based on a percentage of the steady-state value of the signal, but that doesn't work for signals that tend to zero as ##t \rightarrow \infty##. Another defines it based on a percentage of the input level, and a third defines it based on a percentage of the peak level of the signal.
One thing that's common to them all is that, for a second-order system, the real part of the poles only give an approximate idea of what the settling time of the system is.
If we just initially ignore the fast pole and just approximate your closed-loop system as a second-order system with a zero at ##s = 0##, then its step response will have the form:
$$
c(t) = \frac{\omega_n}{\sqrt{1 - \zeta^2}}e^{-\zeta\omega_n t}\sin\left(\sqrt{1 - \zeta^2}\omega_n t\right)
$$
We could, for instance, define the settling time of the system as the time it takes for ##|c(t)| \leq 0.05##, i.e. 5 % of the input level.
At three time constants ##t = 3\tau = \frac{3}{\zeta\omega_n}##, you have ##e^{-\zeta\omega_n t} = e^{-3}\approx 0.0498##, so the amplitude of the sinusoid has decayed to less than 5 % of its initial value, but that doesn't mean its value is less than 0.05. For ##\zeta## close to 1, i.e. what you get in your example when you adjust ##K_1## so the complex conjugate pair of poles converge on the real axis, the initial amplitude could be huge.
It's a pretty safe bet, though, that if you're comparing a bunch of stable second-order systems with approximately the same time constant, then their outputs will have all settled after five time constants, regardless of damping ratio.
In short: The real part of the closed-loop poles isn't necessarily a good indicator of settling time if you want to compare second-order systems with significant differences in damping ratio.
This is further complicated by the fact that the addition of the fast pole alters the amplitude and introduces a phase shift of ##c(t)##, i.e. the output will have the form:
$$
c(t) = Ae^{-\zeta\omega_n t}\sin\left(\sqrt{1 - \zeta^2}\omega_n t + \phi\right)
$$
where ##A## and ##\phi## will depend on the location of the fast pole, which in turn depends on ##K_1##.
Could you include a picture of the full problem statement? I'd guess you're just supposed to determine ##K_1## by trial and error.