Fermi-dirac distribution

[magnifik]

An electron state has energy 0.14 eV above the Fermi energy. What is the probability that the electron state will be occupied at T = 200K?

do i just use the following formula?

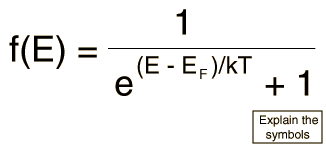
the part that throws me off is the "above the Fermi energy" bit. would i just plug that number in for E - E_f??

 

[CompuChip]

Yep, it means that E = E_F + 0.14 eV, so E - E_F = 0.14 eV.