How can I calculate the energy needed for ferromagnetic hysteresis?

[Tomsk]

Homework Statement

It's a past paper question, but I just don't understand it. I must have missed something here...

The figure [I can't find a decent one to put here] shows a coil of copper wire wrapped around a torus of material. The copper wire makes N turns and carries a current I. The torus has major radius R and minor radius r, where r<<R. Assume that the magnetic is entirely within the material.
(a) The material has a small, constant, positive magnetic susteptibility $$\chi$$. Obtain expressions for the H and B fields. [5 marks]
(b) The material is ferromagnetic but owing to heat treatment it is initially unmagnetized.

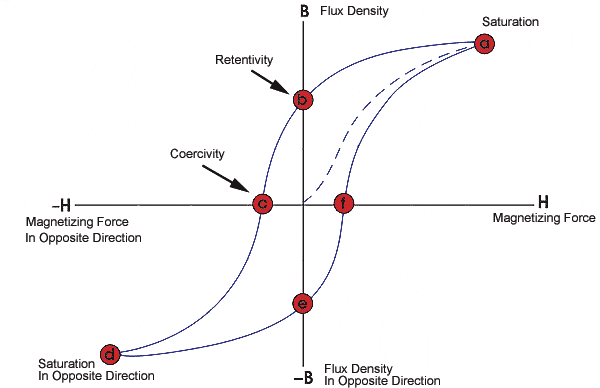
The graph [this is just one I got off the internet, not the actual one] shows the experimentally measured relationship between H and B as the material is first magnetized along the dotted curve to point a, then taken around the hysteresis loop. Given that R = 0.2m and r=0.02m estimate the energy needed to magnetize the material and the energy needed to take the material around the hysteresis loop. (on the actual graph, H stays between +-5*10^4 Am^-1 and B stays between 1.5 and -1.5 T) [7 marks]

Homework Equations

Maxwell's equations, $$\frac{B}{\mu_{0}} = H + M$$, $$M=\chi H$$ change in stored energy = H.dB

The Attempt at a Solution

(a) $$\nabla\times H = J_{free}$$(because$$\epsilon_{0} \partial D/\partial t = 0$$)
$$\int H.dl = \int J.dA$$
$$H.2\pi R = NI$$
$$H=\frac{NI}{2\pi R}$$
$$B=\mu_{0}(1+\chi)H$$
$$B=\mu_{0}(1+\chi)\frac{NI}{2\pi R}$$
Is that OK?

(b)This is where I get stuck. I'm just not sure how it works. Is that curve parameterised by time, or not? I.e, does the system move round the curve automatically once you switch on the current (and have moved it from its equilibrium position) because of the magnetization (if so how?), in the way that a pendulum tries to get to it's equilibrium position, or do you have to adjust the current (or something else?) to change the applied magnetic field, and when you do you find that it moves around that curve? And how do I get from there to the energy required?

 

[Meir Achuz]

You can't use the susceptiblity in ferromagnetism.
The energy is given by \integral H.dB, the area under the hysteresis curve.

 

[Tomsk]

Thanks for the reply. Why can I not use susceptibility? I can't think why they would have given it to me otherwise... And would I want to find an equation for B in terms of H, and integrate that, or do I just work out the area approximately by looking at the graph? I would have thought that wouldn't be very accurate...

 

[Meir Achuz]

The ratio B/H is different for every point on the curve.
The susceptibility was given only for part a.
There is no equation for the curve since it is different for different materials.
You do have to just find the appropriate area.