- #1
learn.steadfast
- 59
- 2
I'm reviewing relativity and am working simple problems to test my understanding. I am reviewing Feynman's HTML book on physics. I don't get the same answer as him for the shape of an E field in a moving particle in one dimension, equation 26.11, but I do get his answer for equation 26.10; and I'm not sure what I'm doing wrong.
http://www.feynmanlectures.caltech.edu/II_26.html
How I worked the problem:
My understanding is that when an object moves at a uniform velocity in the x direction with observers seeing the object move at that velocity; The size of the object and it's fields are supposed to be contracted in the direction of motion; (Eg: according Einstein/Leopold/Infield in another book I read.) The contraction is ONLY in the direction of motion. However, one must also account for the total energy of the object in motion which is a scalar factor determined by the objects speed relative to the measuring frame of reference. So, I looked for all energies and masses that need to be scaled, and I found one reference to energy.
An Electric field is measured by checking the force on a test charge as it's moved in the field. Classical physics would show that force is proportional to the change in energy of the test charge with respect to it's position in the field. [itex] F \propto { {d U} \over { d r }} [/itex] Since the energy falls off as [itex]1 \over r[/itex] the force field must fall off as [itex]1 \over r^2[/itex]
The rest frame equation for the magnitude of a vector electric field (force field) is just:
[itex] |E| ={q \over { 4 \pi \epsilon_0 } } \cdot { 1 \over x^2 + y^2 + z^2 } [/itex] . because . [itex] r^2 = x^2 + y^2 + z^2 [/itex]
Modifying the rest frame equation by accounting for energy scaling and Lorentz transformations ought to allow me to write down down (by inspection) an equation for a moving charge's E field as seen by an outside observer.
In Feynman's example, the point charge is uniformly moving in the x direction with velocity v (as a fraction of the speed of light, v=1 is the same as v=c).
From what I learned from Einstein's book, I think the magnitude of the E field of the moving charge should be the rest frame equation scaled by the motion energy to rest energy factor: [itex] 1 \over \sqrt { 1-v^2 } [/itex] . The only other change needed is the Lorentz transformation for x. [itex] x' = { { x - v t } \over \sqrt ( 1-v^2 ) } [/itex]
Therefore, a moving charge's E-field as measured by a rest frame observer ought to be:
[itex] |E| ={{ q \cdot { 1 \over \sqrt {1-v^2} }} \over { 4 \pi \epsilon_0 } } \cdot { 1 \over ({ x-v t \over \sqrt {1 - v^2}})^2 + y^2 + z^2 } [/itex]
When measuring along axii having origin on the moving charge, the direction of the vector E is purely pointing along the axii. (see Feynman's drawings).
Therefore, I should be able to get Feynman's equation 26.10 by setting x = v t in my equation.
[itex]E ={{ q \cdot { 1 \over \sqrt {1-v^2} }} \over { 4 \pi \epsilon_0 } } \cdot { 1 \over { y^2 + z^2 }} [/itex]
Which is clearly the same as Feynman's result.
However, if I set y and z to zero, to try and get equation 26.11, I get:
[itex]
E
={{ q \cdot { 1 \over \sqrt {1-v^2} }} \over { 4 \pi \epsilon_0 } } \cdot { 1 \over ({ x-v t \over \sqrt {1 - v^2}})^2 }
={{ q \cdot { 1 \over \sqrt {1-v^2} }} \over { 4 \pi \epsilon_0 } } \cdot { \sqrt {1 - v^2} ^2 \over ({ x-v t })^2 }
= { q \over { 4 \pi \epsilon_0 } } \cdot { \sqrt {1 - v^2} \over ({ x-v t })^2 }
[/itex]
And that looks different than this screen-shot, February 2018, of the Feynman lectures.
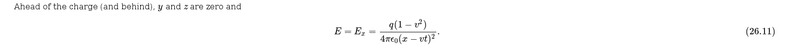
Is there some reason that the Lorentz transformation cancels out the total energy multiplication factor? Or is this just a typo in the online transcription of Feynman's book?
http://www.feynmanlectures.caltech.edu/II_26.html
http://www.feynmanlectures.caltech.edu/II_26.html
How I worked the problem:
My understanding is that when an object moves at a uniform velocity in the x direction with observers seeing the object move at that velocity; The size of the object and it's fields are supposed to be contracted in the direction of motion; (Eg: according Einstein/Leopold/Infield in another book I read.) The contraction is ONLY in the direction of motion. However, one must also account for the total energy of the object in motion which is a scalar factor determined by the objects speed relative to the measuring frame of reference. So, I looked for all energies and masses that need to be scaled, and I found one reference to energy.
An Electric field is measured by checking the force on a test charge as it's moved in the field. Classical physics would show that force is proportional to the change in energy of the test charge with respect to it's position in the field. [itex] F \propto { {d U} \over { d r }} [/itex] Since the energy falls off as [itex]1 \over r[/itex] the force field must fall off as [itex]1 \over r^2[/itex]
The rest frame equation for the magnitude of a vector electric field (force field) is just:
[itex] |E| ={q \over { 4 \pi \epsilon_0 } } \cdot { 1 \over x^2 + y^2 + z^2 } [/itex] . because . [itex] r^2 = x^2 + y^2 + z^2 [/itex]
Modifying the rest frame equation by accounting for energy scaling and Lorentz transformations ought to allow me to write down down (by inspection) an equation for a moving charge's E field as seen by an outside observer.
In Feynman's example, the point charge is uniformly moving in the x direction with velocity v (as a fraction of the speed of light, v=1 is the same as v=c).
From what I learned from Einstein's book, I think the magnitude of the E field of the moving charge should be the rest frame equation scaled by the motion energy to rest energy factor: [itex] 1 \over \sqrt { 1-v^2 } [/itex] . The only other change needed is the Lorentz transformation for x. [itex] x' = { { x - v t } \over \sqrt ( 1-v^2 ) } [/itex]
Therefore, a moving charge's E-field as measured by a rest frame observer ought to be:
[itex] |E| ={{ q \cdot { 1 \over \sqrt {1-v^2} }} \over { 4 \pi \epsilon_0 } } \cdot { 1 \over ({ x-v t \over \sqrt {1 - v^2}})^2 + y^2 + z^2 } [/itex]
When measuring along axii having origin on the moving charge, the direction of the vector E is purely pointing along the axii. (see Feynman's drawings).
Therefore, I should be able to get Feynman's equation 26.10 by setting x = v t in my equation.
[itex]E ={{ q \cdot { 1 \over \sqrt {1-v^2} }} \over { 4 \pi \epsilon_0 } } \cdot { 1 \over { y^2 + z^2 }} [/itex]
Which is clearly the same as Feynman's result.
However, if I set y and z to zero, to try and get equation 26.11, I get:
[itex]
E
={{ q \cdot { 1 \over \sqrt {1-v^2} }} \over { 4 \pi \epsilon_0 } } \cdot { 1 \over ({ x-v t \over \sqrt {1 - v^2}})^2 }
={{ q \cdot { 1 \over \sqrt {1-v^2} }} \over { 4 \pi \epsilon_0 } } \cdot { \sqrt {1 - v^2} ^2 \over ({ x-v t })^2 }
= { q \over { 4 \pi \epsilon_0 } } \cdot { \sqrt {1 - v^2} \over ({ x-v t })^2 }
[/itex]
And that looks different than this screen-shot, February 2018, of the Feynman lectures.
Is there some reason that the Lorentz transformation cancels out the total energy multiplication factor? Or is this just a typo in the online transcription of Feynman's book?
http://www.feynmanlectures.caltech.edu/II_26.html
Attachments
Last edited: