musicgold
- 303
- 19
- Homework Statement
- This is not a homework problem.
I am reading a proof and not sure why a particular step is taken / not taken.
- Relevant Equations
- why is there no axiom like X . 0 = 0
Please refer to the screenshot below. Every step is justified with an axiom. Please see the link to the origal document at the bottom.
I am trying to understand why the proof was not stopped at the encircled step.
1. Is there no axiom that says ## x \cdot 0 = 0 ## ?
2. Isn't the sixth step using the fact that a 0 can be represented by ## x \cdot 0 ## ?
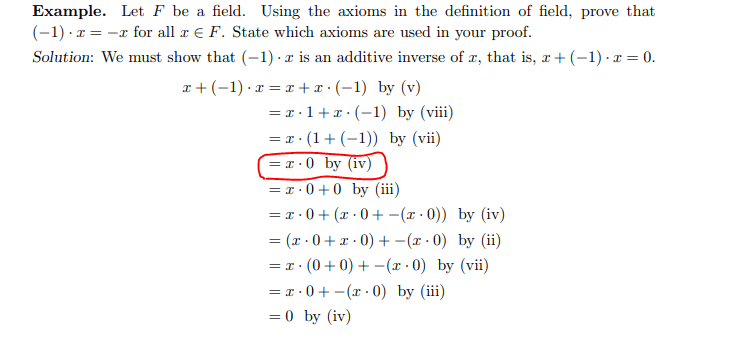 Document
Document
I am trying to understand why the proof was not stopped at the encircled step.
1. Is there no axiom that says ## x \cdot 0 = 0 ## ?
2. Isn't the sixth step using the fact that a 0 can be represented by ## x \cdot 0 ## ?
Last edited: