Finals Study Time A Two Source Circuit w/Inductor, Cap, and Resistor

[Lapse]

Homework Statement

Homework Equations

Z = √(X_C² + X_L²)
X_L = 2πƒL
X_C = 1 / 2πƒC
I = V/Z

The Attempt at a Solution

First off, thank you for all of the help this semester. I'm sure you'll be seeing questions from me in the spring also. Here is how I'm thinking about this problem:

1. Using the above equations, I find the reactances of the inductor and capacitor to be 3141.59Ω and 1.59Ω, respectively.

2. Add: X_L + (-X_C) = 3140Ω = Z

Note: I used -X_C because on a graph the capacitor's reactance would be a downward pointing vector. However, no matter if I add or subtract these reactances the final current would be equivalent since 1.59Ω is much, much smaller than 3141.59Ω.

3. I find the current by using the equation of V/Z; however, the issue is that I have two voltage sources-- so which V do I use?

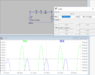
I decided that I could use superposition. So first equation: I = 1.2V / 3140 = .382mA. Second equation: 0.8V / 3140 = .255mA

4. Now I superimpose them. Since the 1.2V source moves rightward and the 0.8V source moves leftward, I did the following:
→ ← →
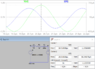
.382 - .255 = .127mA5. My final result seems to be off. Relative to the voltage through the 1.2V source, here is the graph:

As you can see, the difference is 56μA, or about .056mA at the voltage peak of the 1.2V source.

One thing I noticed I did wrong is that the current of .127mA would be present when at the voltage peak of a single source circuit. Since I have 2 voltage sources the way I compared my current to my voltage peak doesn't make sense.

If someone could highlight where I am going wrong I would be very appreciative. The finals are on Wednesday and I've been studying for 6hrs so I'm going to head to bed and check on this in the AM. Thanks :)

 

[gneill]

Check your capacitor impedance. On the circuit diagram the capacitor's value is specified as 200p. Note the p.

Edit:
Also note that VR is shown to have a (very) small phase difference to VL:

You might want to show that this makes negligible difference to the results.

 

[gneill]

As you can see, the difference is 56μA, or about .056mA at the voltage peak of the 1.2V source.

One thing I noticed I did wrong is that the current of .127mA would be present when at the voltage peak of a single source circuit. Since I have 2 voltage sources the way I compared my current to my voltage peak doesn't make sense.

You really can't compare voltages and currents in that fashion. They have different units. What you can do though is find the phase difference. What's the phase angle of the current with respect to the VL voltage source?

 

[Lapse]

Ahh okay... so I had the wrong impedance for the capacitor.

So Z = 1975.62Ω

"What's the phase angle of the current with respect to the VL voltage source?"

Φ = tan-1 (.000607A/1.2V) = .029°

That amplitude comes from dividing 1.2 volts by 1975.62Ω

This angle doesn't seem right. Whats my next step?

 

[gneill]

Ahh okay... so I had the wrong impedance for the capacitor.

So Z = 1975.62Ω

That would be its reactance, 1/(ωC). Its impedance would be 1/(jωC) = -j 1975.65 Ω. Note that impedances are complex values, and that for ideal inductors and capacitors they are entirely imaginary with no real component.

"What's the phase angle of the current with respect to the VL voltage source?"

Φ = tan-1 (.000607A/1.2V) = .029°

That amplitude comes from dividing 1.2 volts by 1975.62Ω

This angle doesn't seem right. Whats my next step?

It is not right. You need to first find the current in its complex form. Voltage divided by total impedance (complex values!). The angle will be extracted from that.

 

[Lapse]

I guess I'm just not understanding what to do with the imaginary number.

So the reactance of the capacitor is = 1975.62Ω, whereas its impedance is -j1975.62Ω... got it.

Now what? Would the next step be to find the phase angle? I could divide the above reactance by the resistance and use tan-1 to get 57.86°, but I'm not sure what this angle is really representing. I know that a phase shift is the degree to which one sine wave is leading or lagging another sine wave.

Is phase angle the same as phase shift? Probably not, since they use two different symbols: Φ vs θ.

 

[gneill]

I guess I'm just not understanding what to do with the imaginary number.

So the reactance of the capacitor is = 1975.62Ω, whereas its impedance is -j1975.62Ω... got it.

Now what? Would the next step be to find the phase angle? I could divide the above reactance by the resistance and use tan-1 to get 57.86°, but I'm not sure what this angle is really representing. I know that a phase shift is the degree to which one sine wave is leading or lagging another sine wave.

You want to compute the current using the voltage and impedances. The result will be a complex value. Convert to polar form (magnitude and angle). The angle is the phase angle referenced to the voltage supply.

Is phase angle the same as phase shift? Probably not, since they use two different symbols: Φ vs θ.

I've seen people use them interchangeably, along with the symbols.

 

[Lapse]

You want to compute the current using the voltage and impedances. The result will be a complex value. Convert to polar form (magnitude and angle). The angle is the phase angle referenced to the voltage supply.

Which voltage? I have two voltage sources. I would have already solved this problem if it were only one.

 

[gneill]

Which voltage? I have two voltage sources. I would have already solved this problem if it were only one.

If you write KVL around the loop you will find that the two sources sum to a single equivalent voltage source (again, counting the minuscule phase angle they've given VR as irrelevant). Or do as you did before and use superposition (more work though).

The question asked to sketch the current relative to VL, which means letting VL set the reference for phase angles throughout the circuit.

 

[Lapse]

Here's where I'm at so far:

Z = √(1k)² + (1550)² = 1845Ω

KVL: 1.2V - 1845ΩI -0.8V = 0 ; I = 217μA

You said it should be a complex answer, so should the current actually be j217μA?

If this is correct, what would be my next step? You said to convert it to polar form. This is where my understanding of j is shaky. How do I convert from complex to polar?

 

[gneill]

You said it should be a complex answer, so should the current actually be j217μA?

No, the current will have a phase angle that depends upon the combined impedance of the reactive components (Inductor and capacitor).

You can work with reactances as you've done, but figuring out the phase angle becomes tricky; You need to look at the net resistance and net reactance and determine what the division does to the resulting phase angle. My old brain doesn't like to wrestle with that sort of puzzle when a more "mechanical" solution is available.

If you keep all the impedances in complex form for your calculations then the resulting current will be in complex form also. From that you can extract the magnitude and phase of the current. So the impedance of the capacitor is $Z_C=-j\;1.592\;k\Omega$, the impedance of the inductor is $Z_Lj\;3.142\;k\Omega$. The resistance impedance is purely real, so $Z_R = 1\;k\Omega$. The current is then:
$$I = \frac{VL-VR}{Z_L + Z_R+Z_C}$$
This will result in the current in complex form (a so-called phasor value).

Converting to polar form (magnitude and angle) is a matter of a bit of Pythagoras and trigonometry. It's the same as finding the magnitude and angle of a vector. The magnitude is the square root of the sum of squares of the component magnitudes, while the angle is the arctan of the ratio of the components (be sure to check the quadrant that the "vector" lies in).

If you have some arbitrary complex number $z = (a + bj)$ then

Magnitude: $|z| = \sqrt{a^2 + b^2}$
Angle: $\phi = \arctan(b/a)$ but check the quadrant! Look at the signs associated with the "x" and "y" values.

Edit: alternatively, if your calculator supports it, use the atan2() function which automatically handles the quadrant placement when working out the angle.

 

[Lapse]

If you keep all the impedances in complex form for your calculations then the resulting current will be in complex form also. From that you can extract the magnitude and phase of the current. So the impedance of the capacitor is $Z_C=-j\;1.592\;k\Omega$, the impedance of the inductor is $Z_Lj\;3.142\;k\Omega$. The resistance impedance is purely real, so $Z_R = 1\;k\Omega$. The current is then:
$$I = \frac{VL-VR}{Z_L + Z_R+Z_C}$$
This will result in the current in complex form (a so-called phasor value).

Converting to polar form (magnitude and angle) is a matter of a bit of Pythagoras and trigonometry. It's the same as finding the magnitude and angle of a vector. The magnitude is the square root of the sum of squares of the component magnitudes, while the angle is the arctan of the ratio of the components (be sure to check the quadrant that the "vector" lies in).

If you have some arbitrary complex number $z = (a + bj)$ then

Magnitude: $|z| = \sqrt{a^2 + b^2}$
Angle: $\phi = \arctan(b/a)$ but check the quadrant! Look at the signs associated with the "x" and "y" values.

Here goes:

VL - VR = 0.4V
Z_L + Z_R + Z_C = j3.142kΩ + 1kΩ + -j1.592kΩ = j2550

i = 0.4 / j2250 ←a current in complex form

I'm not sure how to get the above equation into the form z = a + bj

I can find the magnitude and arctan after that.

 

[gneill]

Here goes:

VL - VR = 0.4V
Z_L + Z_R + Z_C = j3.142kΩ + 1kΩ + -j1.592kΩ = j2550

What happened to the real 1kΩ? You cannot just add real and imaginary components. Your total impedance should be a value with both real and imaginary parts. The resistance will appear as the real part. The sum of the impedances of the inductor and capacitor will appear as the imaginary part.

 

[Lapse]

Oh whoops left that out: i = 0.4V / (1kΩ + j1.55kΩ)

 

[gneill]

Okay! What's the resulting current?

 

[Lapse]

Okay! What's the resulting current?

Well, I'm thinking the denominator is: √1k² + 1.55k² = 1844.59
arctan 1.55/1k = 57.17°

Thus... i = 0.4 / 1.845k∠57.17°

I'm not sure if there should be some angle in the numerator to be divided. 0.4 / 1.845 = .217mA

So is the answer i = .217mA∠57.17° ?

 

[The Electrician]

Well, I'm thinking the denominator is: √1k² + 1.55k² = 1844.59
arctan 1.55/1k = 57.17°

Thus... i = 0.4 / 1.845k∠57.17°

I'm not sure if there should be some angle in the numerator to be divided. 0.4 / 1.845 = .217mA

So is the answer i = .217mA∠57.17° ?

Except that your angle should be the negative of what you have. Moving the angle from the denominator to the numerator changes the sign.

 

[Lapse]

Ahh, which means it leads the voltage, correct?

So, what does 217uA represent with regards to a graph? Because when I plot in LTSpice, the peak amplitude is about 450uA.

I'm thinking it is when the voltage is at 0.4V.

 

[gneill]

At 450 μA the driving voltage is more likely to be VR alone (0.8 V).

 

[Lapse]

At 450 μA the driving voltage is more likely to be VR alone (0.8 V).

Right, but what is the 217uA representing since this is my answer?

 

[gneill]

Right, but what is the 217uA representing since this is my answer?

That's the magnitude of the current running through the components. The angle is the phase shift (or offset) of the current versus VL's assumed zero phase.

Here's a plot showing VL (green) and I (blue):

Yeah, probably should have plotted current in red to better show up

 

[Lapse]

I can see it fine. I appreciate all your help! I guess I just need to understand one more thing:

How did you know that you should subtract VR from VL? Is it based on the voltage source you are finding?
So then, if we were finding current with regards to VR we would say VR - VL = -0.8V ... correct?

The bottom makes sense because if we add up the impedance vectors we get our equivalent resistance, which gives us our standard Ohm's Law equation:
I = V/R.
If I understand correctly, the complex number j is important because it helps us determine lead or lag. A final j in the denominator gave us a negative value for the angle, which tells us that the current was leading the voltage.

Edit:

I am having one other problem. How do I graph for the current as you have? The only options in LTSpice is to click one of the components and see it's current.

 

[gneill]

How did you know that you should subtract VR from VL? Is it based on the voltage source you are finding?

I did a "KVL walk" around the loop (clockwise) and found that VR is opposing VL.

So then, if we were finding current with regards to VR we would say VR - VL = -0.8V ... correct?

You first must define the assumed direction of the current. I took it to be defined to be positive going clockwise around the loop (just a habit I have; it could be taken to be counterclockwise just as easily, it's only an assumed direction. As long as we're consistent in applying the circuit laws the math will sort everything out for us. If the current calculated turns out to be negative, then we made an incorrect assumption about its direction. No big deal. The calculated magnitude will be the same). As it happens my choice was reasonable as VL happens to be larger than VR, so current will be driven clockwise around the loop. Huzzah!

Whether you are comparing the current phase to VL or VR, the current will be the same in either case, being produced by the combined effects of both VL and VR. The reason that VR was plotted was that's what the question wanted as the reference. By "the reference" I mean the defined reference against which we are to specify phase angles. The relative magnitudes of the voltage source and current are largely irrelevant for comparing phase angles. The reference is almost always taken to define the zero angle for phase. (sometimes professors take strange delight in defining an otherwise impractical phase reference. Probably to exercise our complex number algebra )

You can plot VR instead, but since it's phase is essentially identical to that of VL it won't make a perceptible difference (I don't know how you could even see an angular difference of 250 nano-degrees on a clumsy plot like this). You'll have to decide whether to plot VR or -VR. I'd go with -VR since that's the way the term would show up in my KVL walk clockwise around the loop.

If I understand correctly, the complex number j is important because it helps us determine lead or lag. A final j in the denominator gave us a negative value for the angle, which tells us that the current was leading the voltage.

A negative phase angle for the current implies that the load is effectively capacitive, where current leads the voltage, yes! Well spotted.

Edit: A thinking lapse on my part. I was thinking impedance and writing current. A negative phase angle for current implies that the current is lagging behind the voltage. When the voltage phase is at zero degrees, the current still has some time to go before it reaches zero. When you find a lagging current you will find that the impedance of the load has an inductive (positive) reactance. If the current leads, the load has a capacitive (negative) reactance.

Complex arithmetic automatically takes care of all the phase angle relationships and you can use all the circuit analysis techniques that you learned for DC circuits. Yes, it's a pain to work through by hand, converting back and forth from Cartesian to Polar forms to do the math. But it's actually much better than working directly with reactance figures and juggling phase angles for individual components. On a more complicated circuit than the one being analyzed here it would be a brain-mushing nightmare. Get used to doing complex calculations. Obtain a calculator that does complex math, would be my recommendation .

I am having one other problem. How do I graph for the current as you have? The only options in LTSpice is to click one of the components and see it's current.

Yes, that's how it's done. Since the current in a series circuit is identical for every component, there's no issue, right?

 

[Lapse]

Yes, that's how it's done. Since the current in a series circuit is identical for every component, there's no issue, right?

 

[gneill]

I don't know what setting I can't see in your simulation, but a basic simulation with nothing fancy (no hidden parameter changes) yields for me:

Can you upload your .asc file from LTSpice?

 

[Lapse]

When I try I get this error.
However, I haven't changed any settings so everything would be at the stock setup for LTSpice.

 

[gneill]

Change the file type to txt. Or paste it into "code" block. See the BBcode guide:

https://www.physicsforums.com/help/bb-codes