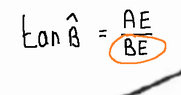Find angle B in the trigonometry problem

[chwala]

Homework Statement

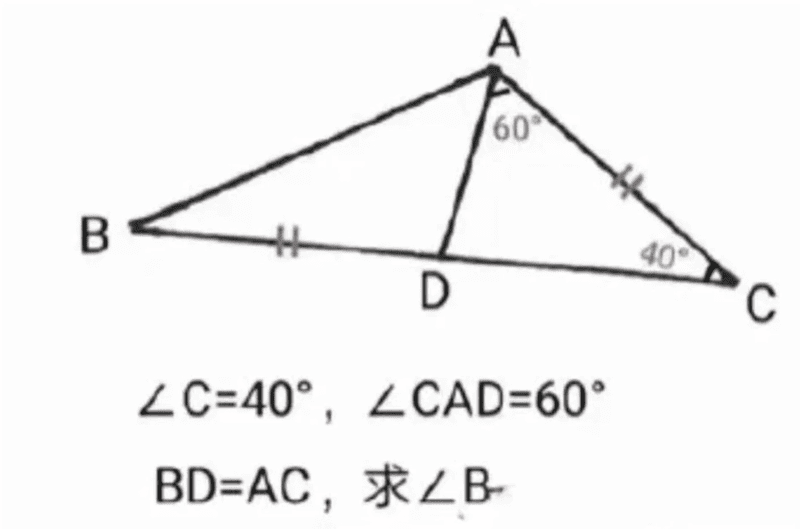
Kindly see the attached problem and find angle $B$

Relevant Equations

sine and cosine rule

Now i was just doing some random study and i saw this problem on the internet. The problem was to find angle $B$

now there were several responses, let me screen shot one that i think was a bit straightforward...

my question is, "is there a much simpler way to find the angle $B$"?

 

[phinds]

my question is, "is there a much simpler way to find the angle $B$"?

What have you tried so far?

 

[chwala]

What have you tried so far?

This is another solution from the internet:

With a slight variation from the attached solution i came up with this:
Following the assumption that $AC=AB=10cm$ then it follows that,
$\frac {10}{sin80}$=$\frac {AD}{sin 40}$
$AD= 6.527cm$
$AB^2$=$10^2+6.527^2-(2×10×6.527×cos 100)$
$AB=12.85cm$
$\frac {12.85}{sin100}$=$\frac {6.527}{sin B}$
$sin B=0.5002210$
$B= sin^{-1}(0.5002210)=30^0$

 

[neilparker62]

Just for a challenge: prove $\tan\hat B=\frac{1}{\sqrt{3}}$. No calculator.

 

[chwala]

Just for a challenge: prove $\tan\hat B=\frac{1}{\sqrt{3}}$. No calculator.

you must be kidding...one may use the equilateral triangle to show this...have a perpendiculor bisector...
...ok let me check it out neil

 

[neilparker62]

You cannot use your destination in your journey - you can't assume 30 degrees at B before you have proven the ratio (no calculator allowed).

 

[chwala]

Find my attempt...i cannot seem to find the ratio that you talked about...

 

[neilparker62]

You have diagonals marked perpendicular in the middle of your construction above. This would be the case if the corresponding quadrilateral is a square. But that's not the case otherwise the diagonals would bisect the corner angles 45/45. I tried geometric constructions and got nowhere so I reverted to trig manipulations to prove the ratio $\tan\hat B=\frac{1}{\sqrt{3}}$ and hence that $\hat B=30^{\circ}$.

 

[chwala]

You have diagonals marked perpendicular in the middle of your construction above. This would be the case if the corresponding quadrilateral is a square. But that's not the case otherwise the diagonals would bisect the corner angles 45/45. I tried geometric constructions and got nowhere so I reverted to trig manipulations to prove the ratio $\tan\hat B=\frac{1}{\sqrt{3}}$ and hence that $\hat B=30^{\circ}$.

Phew it has boggled my mind ...almost 2 hours just looking at this...

 

[neilparker62]

You will need to make use of the "tan rule". See following diagram:

 

[chwala]

Thanks, kindly confirm the dimensions in your diagram, is your $BD= AC$ as indicated in the problem? I do not think so...and further angle $C= 40^0$, i do not see how one can use thinking of right angle (in your case the tangent approach) at this points as the angles in that triangle $ADC$are , $60^0, 80^0$ and $40^0$ respectively (see my post $7$)...how did you come up with the common perpendiculor $BD$?

 

[neilparker62]

It's not at all the same diagram as in the problem - it's a diagram intended to show you how the tan rule works

 

[chwala]

I understand your diagram, it's straightforward...the problem is I do not see how to relate it with the original problem with reasons given... i. e no common perpendicular that will realize two right angle triangles to work with.

 

[neilparker62]

To get BC (in terms of x) you will first need DC (also in terms of x). You can use the sine rule for that.

 

[chwala]

I had seen that...we will need to find length of $DE$ for tangent rule to apply...and I do not think that's possible. I don't think finding $BC$ or $DC$ or $BD$ would help...
How to show proof of your post $4$ without Calculator would be interesting...

 

[neilparker62]

Give some careful thought to what goes where when the tan rule formula is applied to your problem. Alternatively you can actually get an expression for DE in terms of x. In that case you would first need to find AD.

 

[chwala]

Okay, i managed to do this,
$tan 80$=$\frac {AE}{ED}$
and we know that;
$AE=x sin 40^0$ therefore,
$DE$=$\dfrac {x sin 40^0⋅cos 80^0}{sin 80^0}$
$tan B$=$\dfrac {x⋅sin 40^0⋅sin 80^0}{x⋅sin 80^0+x⋅sin 40^0⋅cos 80^0}$.......(1)
$[cos 40^0-cos 120^0]=2sin 80^0sin 40^0$→$0.5[cos 40^0-cos 120^0]=sin 80^0sin 40^0$
$[sin 120^0-sin 40^0]= 2 cos 80^0 sin40^0$→$0.5[sin 120^0-sin 40^0]= cos 80^0 sin40^0$
$tan B$=$\dfrac {-0.5cos 120^0+0.5cos40^0}{sin 80^0+0.5sin 120^0-0.5sin40^0}$
$tan B$=$\dfrac {0.25+0.5 \dfrac {EC}{x}}{\dfrac {AE}{AD}+0.25 \sqrt 3-0.5 \dfrac {AE}{x}}$

alternatively,
$cos 40^0$=$\dfrac {sin 80^0}{2 sin 40^0}$
therefore from (1) above we shall have,
$tan B$=$\dfrac {sin 80^0}{ 2 cos 40^0 +cos 80^0}$ on dividing each term by $sin 80^0$
$tan B$=$\dfrac {1}{\frac {1}{sin 40^0}+\dfrac {cos 80^0}{sin 80^0}}$=$\dfrac {1}{\frac {1}{sin 40^0}+\dfrac {sin 10^0}{sin 80^0}}$
Neil am stuck here mate

 

[neilparker62]

$tan B$=$\frac {sin 80^0}{ 2 cos 40^0 +cos 80^0}$ on dividing each term by $sin 80^0$

Neil am stuck here mate

80 = 120 - 40

 

[chwala]

ok by substituting $80=120-40$ in the equation $tan B$=$\frac {sin 80^0}{ 2 cos 40^0 +cos 80^0}$ and after simplification, i end up with,
$tan B$=$\frac {\sqrt 3 cos 40^0 + sin 40^0}{ 3 cos 40^0+\sqrt 3 sin 40^0}$=$\frac {\sqrt 3 + tan 40^0}{ 3 +\sqrt 3 tan40^0}$=$\frac {1}{ \sqrt 3}$⋅$\frac {\sqrt 3 + tan 40^0}{ \sqrt 3 +tan40^0}$=$\frac {1}{ \sqrt 3}$ Bingo!

 

[neilparker62]

ok by substituting $80=120-40$ in the equation $tan B$=$\frac {sin 80^0}{ 2 cos 40^0 +cos 80^0}$ and after simplification, i end up with,
$tan B$=$\frac {\sqrt 3 cos 40^0 + sin 40^0}{ 3 cos 40^0+\sqrt 3 sin 40^0}$=$\frac {\sqrt 3 + tan 40^0}{ 3 +\sqrt 3 tan40^0}$=$\frac {1}{ \sqrt 3}$⋅$\frac {\sqrt 3 + tan 40^0}{ \sqrt 3 +tan40^0}$=$\frac {1}{ \sqrt 3}$ Bingo!

Mission accomplished!

 

[chwala]

View attachment 287663
Mission accomplished!

Respects to you Neil, you're smart man!

 

[Charles Link]

This problem is interesting. By law of sines, etc. I got
$\tan{B}=\frac{\sin(40)}{1+\frac{\sin(60)}{\sin(80)}-\cos(40)}$.
I set this equal to $\frac{1}{\sqrt{3}}$, and was able to show consistency with a lot of algebra.
Using $\cos(120)=-\frac{1}{2}$ and $\cos(3 \theta)=4 \cos^3(\theta)-3 \cos(\theta)$, we have
$\cos^3(40)=(6 \cos(40)-1)/8$, and I was able to simplify things, but it took a lot of work. It also involved grouping $\sin(40)=\sqrt{1-\cos^2(40)}$ terms together, and squaring both sides. I managed to get it to two expressions with $\cos^2(40),\cos(40)$, and constant terms, and I was able to get both expressions to agree.
Note: $\sin(60)=\sqrt{3}/2$, and $\sin(80)=2 \sin(40) \cos(40)$.

 

[neilparker62]

This problem is interesting. By law of sines, etc. I got
$\tan{B}=\frac{\sin(40)}{1+\frac{\sin(60)}{\sin(80)}-\cos(40)}$.

You can get from here to the expression in post #17 by writing sin(60) as sin(100-40) - noting that sin(100)=sin(80) and cos(100)=-cos(80). Begin by multiplying through by sin(80).

 

[Charles Link]

You can get from here to the expression in post #17 by writing sin(60) as sin(100-40) - noting that sin(100)=sin(80) and cos(100)=-cos(80). Begin by multiplying through by sin(80).

This one is interesting in that there still doesn't seem to be a very simple way to get 30 degrees for B. Without a calculator to give us a clue, like in post 3, we wouldn't have guessed that the expressions are indeed that $\tan{B}=\frac{1}{\sqrt{3}}$. (My first instincts were that my expression in post 22 might give something close to 30 degrees, but it wouldn't be exactly 30 degrees).

 

[neilparker62]

 

[Charles Link]

For the last step, I needed an alternative reason: We have the pair of similar triangles:$\frac{ad}{bd}=c_1$ and $\frac{dc}{de}=c_1$, so that $\frac{ad}{bd}=\frac{dc}{de}$. We need to show the other pair are also similar triangles, so that $\frac{bd}{de}=c_2=\frac{ad}{dc}$, for some $c_2$. We can cross-multiply both expressions, and we see that that is indeed the case. :)

Meanwhile, the construction of post 25 is a very clever one. Good solution @neilparker62 :)

 

[neilparker62]

An easier construction is as per following diagram. The reader and/or OP can figure out the similarity of triangles DAE and DBA.

 

[Charles Link]

Very clever @neilparker62 :)

To show the triangles are similar, we need to show $de/da=da/db$. (These are corresponding sides around the same angle).
Now $da/db=da/ac=\sin(40)/\sin(80)$.
Meanwhile $de/da=\sin(30)/\sin(50)$.
We need to show $\sin(40)/\sin(80)=\sin(30)/\sin(50)$.

With $\sin(80)=2 \sin(40) \cos(40)$, and $\sin(30)=1/2$, and $\cos(40)=\sin(50)$, we have proven the triangles to be similar, and thereby angle $B=30$ degrees.

 

[chwala]

Very clever @neilparker62 :)

To show the triangles are similar, we need to show $de/da=da/db$. (These are corresponding sides around the same angle).
Now $da/db=da/ac=\sin(40)/\sin(80)$.
Meanwhile $de/da=\sin(30)/\sin(50)$.
We need to show $\sin(40)/\sin(80)=\sin(30)/\sin(50)$.

With $\sin(80)=2 \sin(40) \cos(40)$, and $\sin(30)=1/2$, and $\cos(40)=\sin(50)$, we have proven the triangles to be similar, and thereby angle $B=30$ degrees.

therefore,
$sin 40=0.5 (2sin 40)$ after the substituting... $cos 40=sin 50$
$→sin 40=sin 40$ thus the two triangles are similar.

 

[neilparker62]

@ Charles Link. Thanks for your kind comment.

@chwala. Thanks for posting the problem - its solution certainly taxed one's geometry and trigonometry skills! I also learned (as an aside) that $\sqrt[9]{1}=e^{i\frac{2\pi}{9}}=\cos\frac{2\pi}{9}+i\sin\frac{2\pi}{9}$

Or in degrees: $\sqrt[9]{1}=e^{i\frac{360^{\circ}}{9}}=\cos40^{\circ}+i\sin40^{\circ}$

That's one of 9 complex roots since technically $\sqrt[9]{1}=e^{in\frac{2\pi}{9}}$.

Came up trying to solve for $\cos40^{\circ}$ by writing $\cos60=\cos(100-40)$.