Find Area of Triangle QLP & XYZ in Hexagon

AI Thread Summary
To find the area of triangles QLP and XYZ within a hexagon formed by three squares attached to the sides of a right-angled triangle, the area can be calculated using the formula A = 1/2 * ab * sin C. The total area of the figure includes the areas of the two squares and the two triangles, which can be rearranged to form a rectangle. The areas of the squares are calculated as a² and b², while the triangles contribute 2 * (1/2 * a * b). The problem is resolved by summing these areas, confirming the approach is effective.
ritwik06
Messages
577
Reaction score
0

Homework Statement



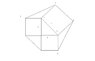
A right angled triangle has 3 squares attached to each side(the measure of each is givn in the figure). a hexagon is thus formed. Find its area.

Homework Equations



none

The Attempt at a Solution


I have found the area of the figure except for the following triangles.
triangle QLP and triangle XYZ
Please help me with these two triangles!
 
Last edited:
Physics news on Phys.org
The figure is here

The figure is here
 

Attachments

  • Question.JPG
    Question.JPG
    10.6 KB · Views: 424
It may help to know that you can find the area of a triangle to be:

A = \frac{1}{2}ab\sin C
 
Last edited:
You want the sum of the areas of four regions:

Two are squares, and two are triangles which together can be repositioned to form a rectangle. a*a, b*b, and two of a*b.
 
Thanks, the problem seems solved. Thanks a lot!
 

Thread 'Family of lines that are at a distance of 5 from the origin'

I picked up this problem from the Schaum's series book titled "College Mathematics" by Ayres/Schmidt. It is a solved problem in the book. But what surprised me was that the solution to this problem was given in one line without any explanation. I could, therefore, not understand how the given one-line solution was reached. The one-line solution in the book says: The equation is ##x \cos{\omega} +y \sin{\omega} - 5 = 0##, ##\omega## being the parameter. From my side, the only thing I could...
View full post »

Similar threads

Finding area of a non right angled triangle
Replies
9
Views
3K
Area of Hexagon - Geometry Challenge
Replies
9
Views
3K
Length of AD inside a triangle ABC
Replies
5
Views
2K
Area of Triangle: Find the Unknown Formula
Replies
9
Views
2K
Area of interior triangle of pyramid normal to a side length
Replies
3
Views
1K
Area of Outer Triangle composed of two inner triangles
Replies
15
Views
3K
Combinatorics: Counting quadrilaterals in triangle pattern
Replies
2
Views
2K
Finding the Distance to a Building with Trigonometry
Replies
4
Views
3K
Prove the sums of the angles of any given triangle = 180°
Replies
12
Views
3K
Finding OA in Triangle Geometry
Replies
9
Views
3K

Hot Threads

Recent Insights

Back
Top