gex
- 36
- 2
The Question:
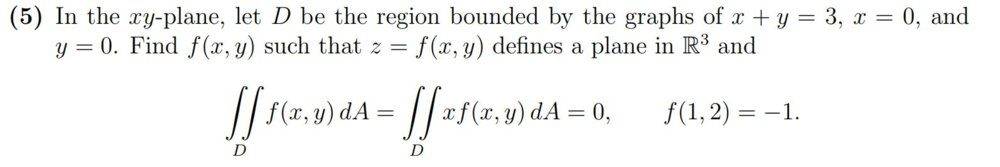
Attempt at a solution:
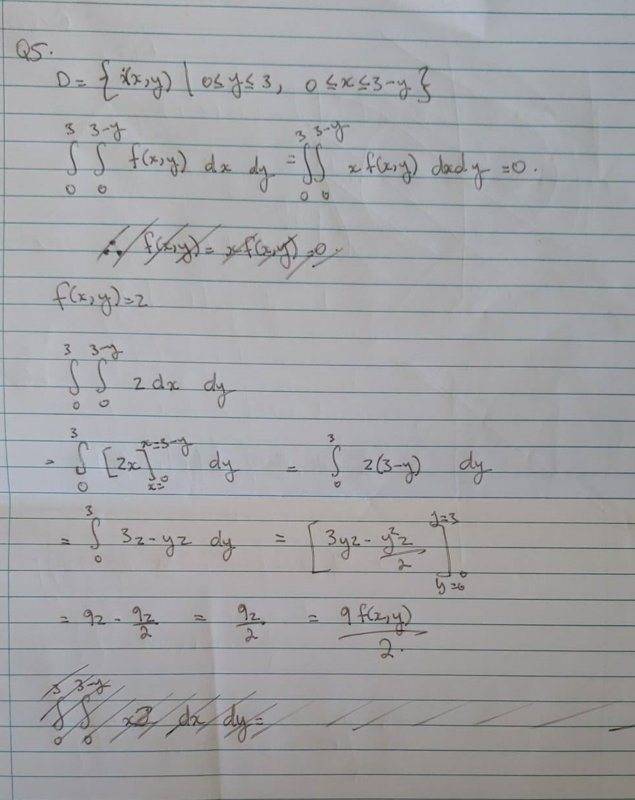
I know for a fact that my attempt is fully wrong, but I am just grasping at straws here and have no clue how to approach this problem. Any help getting me to wrap my head around how to approach this is much appreciated. Thank you in advance.
Attempt at a solution:
I know for a fact that my attempt is fully wrong, but I am just grasping at straws here and have no clue how to approach this problem. Any help getting me to wrap my head around how to approach this is much appreciated. Thank you in advance.