Gweniiix
- 2
- 0
I've been given the following homework exercise and I really need some help with part C.
Question1.
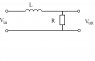
In figure 1. (attachment), an LR-lowpass filter is given with L = 120mH and R = 18 kΩ.
This filter is characterized by the transfer function: H(f) = Vuit(F)/Vin(f)
Determine the following paramters for this filter:
A) The 3dB bandwidth.
I found the answer to this question as follows: R/2∏L = 23.9 kHz
B) The equivalent noise bandwidth.
The answer to this question is: R/4L = 37.5 kHzNow let the input signal of the lowpass filter be a bandlimited noise signal with power spectral density (PSD):
Pn(f) = 1 for f < 140 kHz
0 for f > 140 kHz
C) Determine a new value for L such that 70% of the total available noise power is dissipated in R (100% of the total available noise power is dissipated in R for L =0).
The answer to this question should be: The value of L = 26.9 mH, but I can't figure out why. Can someone please help me?
Question1.
In figure 1. (attachment), an LR-lowpass filter is given with L = 120mH and R = 18 kΩ.
This filter is characterized by the transfer function: H(f) = Vuit(F)/Vin(f)
Determine the following paramters for this filter:
A) The 3dB bandwidth.
I found the answer to this question as follows: R/2∏L = 23.9 kHz
B) The equivalent noise bandwidth.
The answer to this question is: R/4L = 37.5 kHzNow let the input signal of the lowpass filter be a bandlimited noise signal with power spectral density (PSD):
Pn(f) = 1 for f < 140 kHz
0 for f > 140 kHz
C) Determine a new value for L such that 70% of the total available noise power is dissipated in R (100% of the total available noise power is dissipated in R for L =0).
The answer to this question should be: The value of L = 26.9 mH, but I can't figure out why. Can someone please help me?