Joffe
- 36
- 0
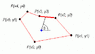
I have a series of points on a 2 dimensional plane that form a polygon.
Somewhere inside the polygon I have another point and an angle that defines a ray. What algorithm would I use to find which interval is first interstected with the ray?
If the point happens to be outside the polygon then I would want to solve which is the second intersection.
I can work this out using algebra and geometry but I was hoping that perhaps using matrices or something there may be a more efficient way suitable for computing quickly.
I have attatched a simple sketch of what I mean. Thanks.
Somewhere inside the polygon I have another point and an angle that defines a ray. What algorithm would I use to find which interval is first interstected with the ray?
If the point happens to be outside the polygon then I would want to solve which is the second intersection.
I can work this out using algebra and geometry but I was hoping that perhaps using matrices or something there may be a more efficient way suitable for computing quickly.
I have attatched a simple sketch of what I mean. Thanks.
Attachments
Last edited: