You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
MHB Find Mean With Multiple Data [Shortcut]
AI Thread Summary
To find the mean with multiple data points, the formula used is \(\overline{x}=\frac{\sum\limits_{k=1}^n\left(x_kf_k\right)}{\sum\limits_{k=1}^n\left(f_k\right)}\). Users expressed confusion about applying this formula to their data samples. An Excel shortcut for this calculation is =SUMPRODUCT(A2:A5, B2:B5) / SUM(B2:B5). However, it was clarified that calculating the mean without multiplying each data point by its frequency is not feasible. The provided formulas represent the simplest method for computing the mean from a frequency table.
Mathematics news on Phys.org
MarkFL
Gold Member
MHB
- 13,284
- 12
Here is the formula:
$$\overline{x}=\frac{\sum\limits_{k=1}^n\left(x_kf_k\right)}{\sum\limits_{k=1}^n\left(f_k\right)}$$
But to compute the mean using the above formula, you will have to essentially do what is shown in the table.
$$\overline{x}=\frac{\sum\limits_{k=1}^n\left(x_kf_k\right)}{\sum\limits_{k=1}^n\left(f_k\right)}$$
But to compute the mean using the above formula, you will have to essentially do what is shown in the table.
susanto3311
- 73
- 0
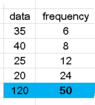
hi Mark, thanks but i confuse how to use your formula...
could you use my data sample (post #1)?
could you use my data sample (post #1)?
I like Serena
Science Advisor
Homework Helper
MHB
- 16,335
- 258
susanto3311 said:hi Mark, thanks but i confuse how to use your formula...
could you use my data sample (post #1)?
Hi susanto3311! Welcome to MHB! :)
The formula for your mean is:
$$Mean = \frac{
\overbrace{35+35+...+35}^{6}
+ \overbrace{40+40+...+40}^{8}
+ \overbrace{25+25+...+25}^{12}
+ \overbrace{20+20+...+20}^{24}
}{6+8+12+24}$$
In your picture each of the sums under an overbrace has been put in a separate cell. The result is calculated afterwards.
In Excel, you can do it in one formula: [m]=SUMPRODUCT(A2:A5, B2:B5) / SUM(B2:B5)[/m].
This is the same formula as the one that Mark gave, just in Excel style. (Wasntme)
susanto3311
- 73
- 0
I like Serena said:Hi susanto3311! Welcome to MHB! :)
The formula for your mean is:
$$Mean = \frac{
\overbrace{35+35+...+35}^{6}
+ \overbrace{40+40+...+40}^{8}
+ \overbrace{25+25+...+25}^{12}
+ \overbrace{20+20+...+20}^{24}
}{6+8+12+24}$$
In your picture each of the sums under an overbrace has been put in a separate cell. The result is calculated afterwards.
In Excel, you can do it in one formula: [m]=SUMPRODUCT(A2:A5, B2:B5) / SUM(B2:B5))[/m].
This is the same formula as the one that Mark gave, just in Excel style. (Wasntme)
i just want, how to find & calculate mean without hard work...
like my picture attach, without multiplication for each data with frequency...
do you have ideas?
Attachments
I like Serena
Science Advisor
Homework Helper
MHB
- 16,335
- 258
susanto3311 said:without multiplication for each data with frequency...
Sorry, but that is not possible. (Dull)
The formulas given are the simplest way to calculate the mean of a frequency table.
Hi,
I was watching the following video. I found some points confusing. Could you please help me to understand the gaps? Thanks, in advance!
Question 1:
Around 4:22, the video says the following.
So for those mathematicians, negative numbers didn't exist. You could subtract, that is find the difference between two positive quantities, but you couldn't have a negative answer or negative coefficients. Mathematicians were so averse to negative numbers that there was no single quadratic...
Insights auto threads is broken atm, so I'm manually creating these for new Insight articles.
In Dirac’s Principles of Quantum Mechanics published in 1930 he introduced a “convenient notation” he referred to as a “delta function” which he treated as a continuum analog to the discrete Kronecker delta. The Kronecker delta is simply the indexed components of the identity operator in matrix algebra
Source: https://www.physicsforums.com/insights/what-exactly-is-diracs-delta-function/
by...
Here I made a terrible mistake of assuming this to be an equilateral triangle and set 2sinx=1 => x=pi/6. Although this did derive the double angle formulas it also led into a terrible mess trying to find all the combinations of sides. I must have been tired and just assumed 6x=180 and 2sinx=1. By that time, I was so mindset that I nearly scolded a person for even saying 90-x. I wonder if this is a case of biased observation that seeks to dis credit me like Jesus of Nazareth since in reality...
Similar threads
- Replies
- 4
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 4
- Views
- 2K
- Replies
- 4
- Views
- 2K
- Replies
- 5
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 3
- Views
- 2K
- Replies
- 11
- Views
- 3K
- Replies
- 1
- Views
- 1K
- Replies
- 5
- Views
- 3K
Hot Threads
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math
-
B What could prove this wrong? I'm having a dispute with friends
- Started by ducknumerouno
- Replies: 94
- General Math
-
B About a definition: What is the number of terms of a polynomial P(x)?
- Started by littlemathquark
- Replies: 48
- General Math
-
B How Many Straight Lines to Connect an N by M Array of Points in a Closed Loop?
- Started by bob012345
- Replies: 25
- General Math
-
B Geometry Puzzle with 20 points in a cross pattern
- Started by bob012345
- Replies: 31
- General Math
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math
![find mean with multiple data [shortcut].png](/data/attachments/291/291421-e8c93287c3cd6f046c7703e2323995bf.jpg?hash=6Mkyh8PNbw)