SUMMARY
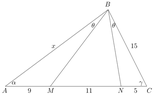
The discussion focuses on calculating side AB of triangle ABC, where BC = 15, AC = 25, and points M and N are defined on AC with specific lengths. The initial assumption of triangle similarity is incorrect, leading to the use of the sine rule in triangles BNC and BMA to derive four equations involving the unknowns x, θ, α, and γ. Ultimately, the solution reveals that side AB measures 22.5 units, with additional values for cos(α) and cos(γ) provided for further analysis.
PREREQUISITES
- Understanding of triangle properties and the sine rule
- Familiarity with trigonometric functions and their applications in geometry
- Basic knowledge of coordinate geometry for triangle representation
- Ability to solve systems of equations involving trigonometric identities
NEXT STEPS
- Study the sine rule in depth, particularly in non-right triangles
- Learn how to apply coordinate geometry to solve geometric problems
- Explore advanced trigonometric identities and their proofs
- Investigate methods for solving systems of equations involving trigonometric functions
USEFUL FOR
Mathematicians, geometry enthusiasts, and students studying trigonometry and triangle properties will benefit from this discussion.