lion_
- 18
- 0
Homework Statement
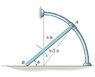
Given: ##\mu_B=0.52##
##\theta=30^{\circ}##
Weight- ##25## lb
##\omega=0##
## l=6## ft
##r_c=3\sqrt 2## radius of curvature.
Homework Equations
My Equations of motion are the following:
##\xleftarrow{+}\sum F_x=N_A\sin 60 - F_B=0##
##\downarrow{+} \sum F_y= N_A \cos 60-N_B+mg=m(a_G)_y##
##\circlearrowright + \sum M_G=2.60N_B-1.5F_B+2.60N_A\cos 60=I_G \alpha##
##(a_G)_y=\alpha r##
##I_G=\frac{1}{12}ml^2##
The Attempt at a Solution
I am not sure what ##r## to use for my ##(a_g)_Y## value
I have tried multipule values of ##r## such as 6,3 and ##r_c## none yield the correct answer.