Homework Help Overview
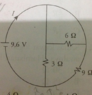
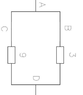
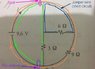
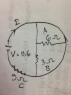
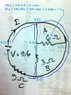
The discussion revolves around finding the current in an electrical circuit involving resistors of 3 ohms, 6 ohms, and 9 ohms. Participants are analyzing the configuration of these resistors, particularly focusing on series and parallel arrangements, and the implications of a short-circuited resistor.
Discussion Character
- Exploratory, Assumption checking, Conceptual clarification
Approaches and Questions Raised
- Participants explore various configurations of the resistors, questioning whether certain resistors are in series or parallel. There are attempts to calculate the current based on different assumptions about the circuit setup.
Discussion Status
The discussion is active, with participants providing insights and questioning each other's reasoning. Some guidance has been offered regarding the implications of the 6 ohm resistor being short-circuited, which has led to further exploration of the circuit's behavior.
Contextual Notes
There is mention of potential discrepancies in provided answer options, and participants are encouraged to verify their calculations against these options. The discussion also highlights the complexity some participants feel regarding the concepts of current division and resistor configurations.
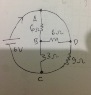
 How do I manage to get this arithmetic wrong?! Yes we could just say the current through the 3 Ω resistor is ##\frac{9.6}{3}## = 3.2 A, and then the flow through the 9 Ω resistor is a third as much = (1 + 0.2/3) adding up to (4.2 + 0.2/3) = 4.26666... ≈ 4.27 A as you say.
How do I manage to get this arithmetic wrong?! Yes we could just say the current through the 3 Ω resistor is ##\frac{9.6}{3}## = 3.2 A, and then the flow through the 9 Ω resistor is a third as much = (1 + 0.2/3) adding up to (4.2 + 0.2/3) = 4.26666... ≈ 4.27 A as you say.