Find the electric field from charge density

[PhysicsTest]

Homework Statement

To calculate the electric field from the charge density inside the BJT.

Relevant Equations

$dE = \frac {dq} {4\pi\epsilon r^2}$

There is a section in the BJT explanation the charge density and the corresponding electric field graphs. But i was not sure how the electric field is derived and hence i started deriving it. Please correct me if my understanding is wrong in posting the question

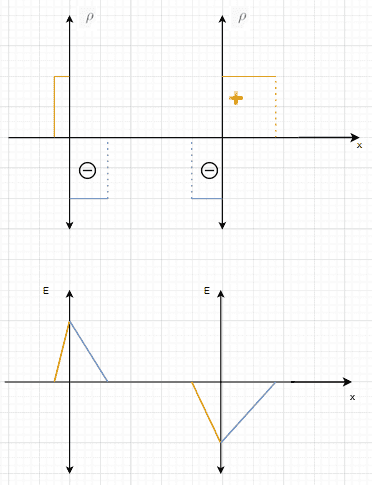
It is an $npn$ BJT. My derivation is
$dE = \frac {dq} {4\pi\epsilon r^2}$
If i only calculate only for the 1st region

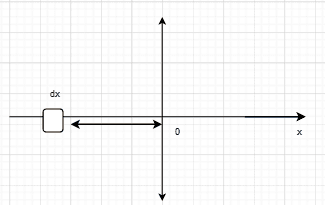
$dq = \rho dx$
I am assuming at some distance x1,
$dE = \int_0^{x1}\frac{\rho dx} {4\pi\epsilon x^2}$
$E = [\frac{\rho} {4\pi\epsilon x}]_0^{x1}$
I am really not sure if I am proceeding properly?

 

[Delta2]

No unfortunately you are not calculating what you want to calculate. The way you setup that integral, what you calculate is the electric field at point 0 (the origin) of a constant linear charge density that extends from the origin to point x1 along the x-axis. But I am sure this is not what you intended to calculate as the charge density inside the transistor is not linear(by linear i mean here one dimensional 1D line) though it is constant.

I believe it is a strategical mistake to use coulomb's law to integrate for the electric field (cause that's what you trying to do here, though you are not doing it correctly). This problem can be solved by using Gauss's law in differential form ,where, instead of calculating an integral, you solve a simple differential equation with proper boundary conditions and some additional assumptions.

 

[Delta2]

Essentially your problem is that of determining the electric field from two slabs of charge density $\rho$ and $-\rho$ that meet along the x-axis. Gauss law in differential form will be for the region of the first slab $$\nabla\cdot\mathbf{E}=\frac{\rho}{\epsilon_0}$$ and for the region of the second slab $$\nabla\cdot\mathbf{E}=\frac{-\rho}{\epsilon_0}$$.

Now the solution to these differential equations with the two slabs having finite dimensions along the x,y,z axis is what i call the coulomb integral that is $$\mathbf{E}=\int_{slab region}\rho \frac{\mathbf{r-r'}}{|\mathbf{r-r'}|^3}d^3\mathbf{r'}$$
However here , instead of calculating this integral over the slab region, we can make some simplifying assumptions that simplify the differential equations and make their solution straightforward. The first differential equation is in cartesian coordinate system $$\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}=\frac{\rho}{\epsilon_0}$$
Now the simplifying assumption is that if the slab of charge density $\rho$ is extending in the y and z directions much more than in the x direction, then we can take $E_y,E_z\approx 0$ and thus the differential equation simplifies to $$\frac{\partial E_x}{\partial x}=\frac{\rho}{\epsilon_0}$$ which is very easy and has straightforward solution.